Page 95 - Entrophy Analysis in Thermal Engineering Systems
P. 95
88 Entropy Analysis in Thermal Engineering Systems
_
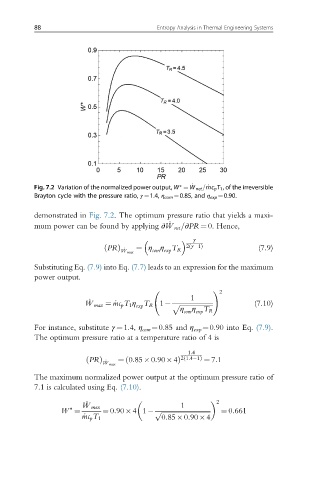
Fig. 7.2 Variation of the normalized power output, W ∗ ¼ W net = _ mc p T 1 , of the irreversible
Brayton cycle with the pressure ratio, γ ¼1.4, η com ¼0.85, and η exp ¼0.90.
demonstrated in Fig. 7.2. The optimum pressure ratio that yields a maxi-
mum power can be found by applying ∂ _ W net =∂PR ¼ 0. Hence,
γ
ð
ð 2 γ 1Þ (7.9)
¼ η η T R
com exp
PRÞ _ W max
Substituting Eq. (7.9) into Eq. (7.7) leads to an expression for the maximum
power output.
! 2
1
(7.10)
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
_ W max ¼ _mc p T 1 η T R 1 p
exp
η η T R
com exp
For instance, substitute γ ¼1.4, η com ¼0.85 and η exp ¼0.90 into Eq. (7.9).
The optimum pressure ratio at a temperature ratio of 4 is
1:4
ð
ð
ð PRÞ _ W max ¼ 0:85 0:90 4Þ 21:4 1Þ ¼ 7:1
The maximum normalized power output at the optimum pressure ratio of
7.1 is calculated using Eq. (7.10).
2
1
∗ _ W max
W ¼ ¼ 0:90 41 ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffip ¼ 0:661
0:85 0:90 4
_ mc p T 1