Page 96 - Entrophy Analysis in Thermal Engineering Systems

Irreversible engines—Closed cycles 89

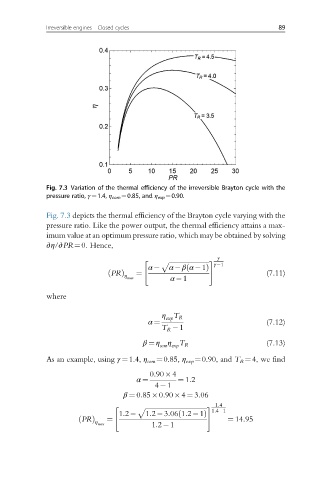
Fig. 7.3 Variation of the thermal efficiency of the irreversible Brayton cycle with the
pressure ratio, γ ¼1.4, η com ¼0.85, and η exp ¼0.90.

Fig. 7.3 depicts the thermal efficiency of the Brayton cycle varying with the
pressure ratio. Like the power output, the thermal efficiency attains a max-
imum value at an optimum pressure ratio, which may be obtained by solving
∂η/∂PR¼0. Hence,
γ
" ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi #
γ 1
p
ð
α α βα 1Þ
ð PRÞ ¼ (7.11)
α 1
η max
where
η T R
exp
α ¼ (7.12)
T R 1
(7.13)
β ¼ η η T R
com exp
As an example, using γ ¼1.4, η com ¼0.85, η exp ¼0.90, and T R ¼4, we find
0:90 4
α ¼ ¼ 1:2
4 1
β ¼ 0:85 0:90 4 ¼ 3:06
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi # 1:4
"
1:4 1
p
1:2 1:2 3:06 1:2 1Þ
ð
ð PRÞ ¼ ¼ 14:95
1:2 1
η max