Page 186 - Essentials of physical chemistry

148 Essentials of Physical Chemistry

A B C kinetics
1200

1000
800
Gallons 600

400

200
0
0 10 20 30 40 50 60
Days
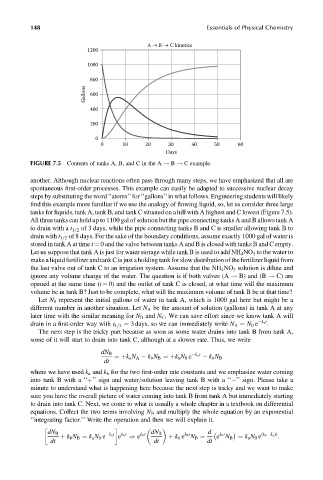
FIGURE 7.5 Contents of tanks A, B, and C in the A ! B ! C example.

another. Although nuclear reactions often pass through many steps, we have emphasized that all are
spontaneous first-order processes. This example can easily be adapted to successive nuclear decay
steps by substituting the word ‘‘atoms’’ for ‘‘gallons’’ in what follows. Engineering students will likely
find this example more familiar if we use the analogy of flowing liquid, so, let us consider three large
tanks for liquids, tank A, tank B, and tank C situated on a hill with A highest and C lowest (Figure 7.5).
All three tanks can hold up to 1100 gal of solution but the pipe connecting tanks A and B allows tank A
to drain with a t 1=2 of 3 days, while the pipe connecting tanks B and C is smaller allowing tank B to
drain with t 1=2 of 8 days. For the sake of the boundary conditions, assume exactly 1000 gal of water is
stored in tank A at time t ¼ 0 and the valve between tanks A and B is closed with tanks B and C empty.
Let us suppose that tank A is just for water storage while tank B is used to add NH 4 NO 3 to the water to
make a liquid fertilizer and tank C is just a holding tank for slow distribution of the fertilizer liquid from
the last valve out of tank C to an irrigation system. Assume that the NH 4 NO 3 solution is dilute and
ignore any volume change of the water. The question is if both valves (A ! B) and (B ! C) are
opened at the same time (t ¼ 0) and the outlet of tank C is closed, at what time will the maximum
volume be in tank B? Just to be complete, what will the maximum volume of tank B be at that time?
Let N 0 represent the initial gallons of water in tank A, which is 1000 gal here but might be a
different number in another situation. Let N A be the amount of solution (gallons) in tank A at any
later time with the similar meaning for N B and N C . We can save effort since we know tank A will
drain in a first-order way with t 1=2 ¼ 3 days, so we can immediately write N A ¼ N 0 e k a t .
The next step is the tricky part because as soon as some water drains into tank B from tank A,
some of it will start to drain into tank C, although at a slower rate. Thus, we write

dN B k a t
¼þk a N A k b N B ¼þk a N 0 e k b N B
dt
where we have used k a and k b for the two first-order rate constants and we emphasize water coming
into tank B with a ‘‘þ’’ sign and water=solution leaving tank B with a ‘‘ ’’ sign. Please take a
minute to understand what is happening here because the next step is tricky and we want to make
sure you have the overall picture of water coming into tank B from tank A but immediately starting
to drain into tank C. Next, we come to what is usually a whole chapter in a textbook on differential
equations. Collect the two terms involving N B and multiply the whole equation by an exponential
‘‘integrating factor.’’ Write the operation and then we will explain it.

dN B k a t k b t k b t dN B k b t d k b t (k b k a )t
þ k b N B ¼ k a N 0 e e ) e þ k b e N B ¼ e N B ¼ k a N 0 e :
dt dt dt