Page 196 - Essentials of physical chemistry

158 Essentials of Physical Chemistry

activated complex is a group of atoms with rubber bands for bonds. In the process which leads to the
product molecule(s), Eyring supposed that the weakest bond in the activated complex would break
and lead to the product(s). There is a point of controversy here. The Eyring transition-state model
assumes that the transition state exists briefly but for a finite time as a unit. More detailed
calculations show that the reaction pathway usually travels through a molecular cluster that has at
least one unstable vibration with an imaginary vibrational frequency due to a ‘‘saddle point’’ in the
energy surface. Other experimental evidence shows that the reaction rate is quantized in steps
according to the positive part of the saddle point with the inverted potential providing the ‘‘pass over
the mountain,’’ so it may be that the Eyring vibrational frequency refers to the quantized energy of
the usual positive potential at the saddle point and not the imaginary frequency part of the saddle
point in the energy surface (Figure 8.2).
Recall that the average energy in the Boltzmann treatment of gases led to the average kinetic
energy of (3=2)RT per mole or (3=2)k B T per molecule, implying (1=2)k B T energy per degree of
freedom in each molecule. Then, consider a vibrating harmonic oscillator as a model for a molecular
vibration. The unusual thing about such an oscillator is that when the vibrational coordinate passes
over the minimum, it has all kinetic energy and no potential energy but when it is at either limit
(turning point) it stops momentarily with no kinetic energy and all potential energy before reversing
direction. Thus, a vibration has both kinetic and potential energy characteristics, and it will be
shown in a later chapter that the energy is proportional to (2=2)k B T since two forms of energy are
present. So, Eyring used the energy of the vibration as E vib ¼ hn ¼ 2k B T=2 ¼ k B T, which is
equivalent to saying

=
n ¼ k B Th,
which has inverse time units.

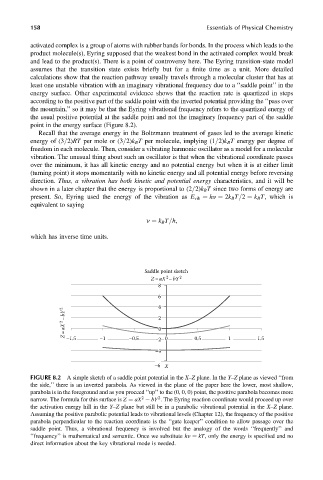
Saddle point sketch
Z= aX –bY 2
2
8
6 4
Z= aX 2 – bY 2 2 0

–1.5 –1 –0.5 0.5 1 1.5
–2 0
–4
X
–6
FIGURE 8.2 A simple sketch of a saddle point potential in the X–Z plane. In the Y–Z plane as viewed ‘‘from
the side,’’ there is an inverted parabola. As viewed in the plane of the paper here the lower, most shallow,
parabola is in the foreground and as you proceed ‘‘up’’ to the (0, 0, 0) point, the positive parabola becomes more
2
2
narrow. The formula for this surface is Z ¼ aX bY . The Eyring reaction coordinate would proceed up over
the activation energy hill in the Y–Z plane but still be in a parabolic vibrational potential in the X–Z plane.
Assuming the positive parabolic potential leads to vibrational levels (Chapter 12), the frequency of the positive
parabola perpendicular to the reaction coordinate is the ‘‘gate keeper’’ condition to allow passage over the
saddle point. Thus, a vibrational frequency is involved but the analogy of the words ‘‘frequently’’ and
‘‘frequency’’ is mathematical and semantic. Once we substitute hn ¼ kT, only the energy is specified and no
direct information about the key vibrational mode is needed.