Page 256 - Essentials of physical chemistry

218 Essentials of Physical Chemistry

‘‘n-space’’ and we note that the n values can be negative so the possible values of this degenerate
n-space forms a surface that tends to be like the surface of a sphere.
2pn
2
L
Thus the number of modes can be written as (# modes) ¼ 2(4p)n dn. Then we use k ¼ to
Ldk
and so we find that the number of nodes per unit volume is
find dn ¼
2p
2

n kL L dk k dk 2p
2
¼ 8p ¼ . Finally we convert back to use c ¼ ln and dk ¼ dn to
V 2p 2p L 3 p 2 c
2
n k dk 1 2pn 2p 8pn dn
2 2
find ¼ ¼ dn ¼ .
V p 2 p 2 c c c 3
Although this is a rather complicated way to count all the nodes in a given volume, it has been
checked over and over and we are telling you the ‘‘right way’’ rather than just making a statement.
This difficult task has a reward however. In the late 1800s, the Boltzmann influence would predict
an average energy per mode of (k B T) for each ‘‘mode’’ since they were due to some sort of oscillator.

k B T
An oscillator intrinsically has 2 ¼ k B T for the combined kinetic and potential degrees of
2
freedom that cannot be separated, so the number of modes per volume should be multiplied by k B T!
So that is simple, after the tedious but correct counting scheme we get the Rayleigh–Jeans formula
n

as ¼ r(n)dn (Figure 10.5). Thus we have
V
2
8pk B Tn dn
:
Rayleigh Jeans ) r(n)dn ¼ 3
c

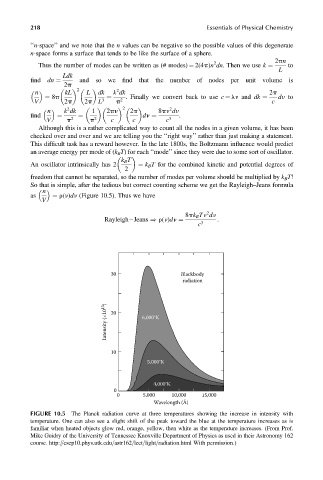
30 Blackbody
radiation

Intensity (×10 13 ) 20 6,000°K

10
5,000°K

4,000°K
0
0 5,000 10,000 15,000
Wavelength (Å)
FIGURE 10.5 The Planck radiation curve at three temperatures showing the increase in intensity with
temperature. One can also see a slight shift of the peak toward the blue at the temperature increases as is
familiar when heated objects glow red, orange, yellow, then white as the temperature increases. (From Prof.
Mike Guidry of the University of Tennessee Knoxville Department of Physics as used in their Astronomy 162
course. http:==csep10.phys.utk.edu=astr162=lect=light=radiation.html With permission.)