Page 245 - Excel for Scientists and Engineers: Numerical Methods

222 EXCEL NUMERICAL METHODS

0.00006%. (Compare this with the 3.6% error in the Euler method calculation at
the same point.) Even after 10 half-lives (not shown), the RK error is only
0.0006%.
In essence, the fourth-order Runge-Kutta method performs four calculation
steps for every time interval. The percent error after one half-life (t = 140) is
only 6 x In contrast, in the solution by Euler's method, decreasing the
time increment to 5 seconds to perform four times as many calculation steps still
only reduces the error to 0.9% after 1 half-life.
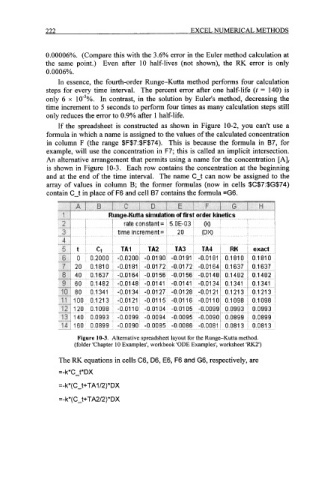
If the spreadsheet is constructed as shown in Figure 10-2, you can't use a
formula in which a name is assigned to the values of the calculated concentration
in column F (the range $F$7:$F$74). This is because the formula in 87, for
example, will use the concentration in F7; this is called an implicit intersection.
An alternative arrangement that permits using a name for the concentration [A],
is shown in Figure 10-3. Each row contains the concentration at the beginning
and at the end of the time interval. The name C-t can now be assigned to the
array of values in column B; the former formulas (now in cells $C$7:$G$74)
contain C-t in place of F6 and cell 87 contains the formula =G6.

Figure 10-3. Alternative spreadsheet layout for the Runge-Kutta method.
(folder 'Chapter 10 Examples', workbook 'ODE Examples', worksheet 'RK2')

The RK equations in cells C6, D6, E6, F6 and G6, respectively, are
=-k*C-t*DX

=-k*(C_t+TAl/2)*DX
=-k*( CWt+TA2/2)*DX