Page 292 - Excel for Scientists and Engineers: Numerical Methods

CHAPTER 12 PARTIAL DIFFERENTIAL EQUATIONS 269

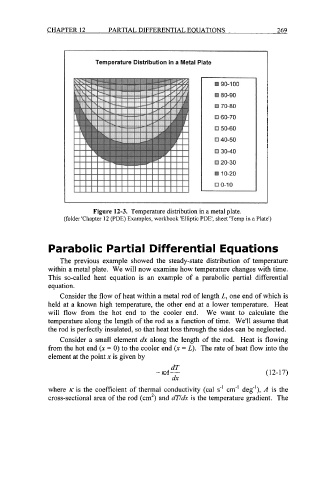
Figure 12-3. Temperature distribution in a metal plate.
(folder 'Chapter 12 (PDE) Examples, workbook 'Elliptic PDE', sheet 'Temp in a Plate')

Parabolic Partial Differential Equations

The previous example showed the steady-state distribution of temperature
within a metal plate. We will now examine how temperature changes with time.
This so-called heat equation is an example of a parabolic partial differential
equation.
Consider the flow of heat within a metal rod of length L, one end of which is
held at a known high temperature, the other end at a lower temperature. Heat
will flow from the hot end to the cooler end. We want to calculate the
temperature along the length of the rod as a function of time. We'll assume that
the rod is perfectly insulated, so that heat loss through the sides can be neglected.
Consider a small element dx along the length of the rod. Heat is flowing
from the hot end (x = 0) to the cooler end (x = L). The rate of heat flow into the
element at the point x is given by
dT
-KA- (1 2- 17)
dx
where K is the coefficient of thermal conductivity (cal s-l cm-' deg-'), A is the
cross-sectional area of the rod (cm2) and dTldx is the temperature gradient. The