Page 303 - Excel for Scientists and Engineers: Numerical Methods

280 EXCEL: NUMERICAL METHODS

Thus a Crank-Nicholson calculation can be set up on a spreadsheet using a
single formula to create the coefficients table, a (different) single formula to
create the constants table, and a single formula for the values table.
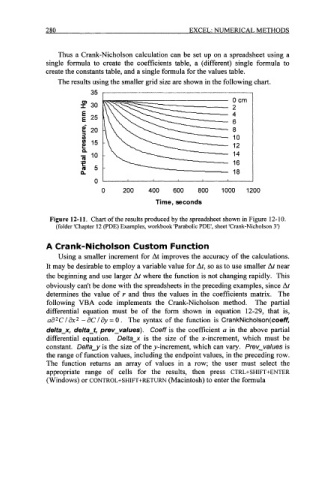
The results using the smaller grid size are shown in the following chart.

0 cm
I" 30 2
4
25
6
E! 20 8
a I0
f 15 12
P
- 10 14
.-
m
5 5 16
a 18
0 200 400 600 800 1000 1200
Time, seconds

Figure 12-11. Chart of the results produced by the spreadsheet shown in Figure 12-10.
(folder 'Chapter 12 (PDE) Examples, workbook 'Parabolic PDE', sheet 'Crank-Nicholson 3')

A Crank-Nicholson Custom Function
Using a smaller increment for At improves the accuracy of the calculations.
It may be desirable to employ a variable value for At, so as to use smaller At near
the beginning and use larger At where the function is not changing rapidly. This
obviously can't be done with the spreadsheets in the preceding examples, since At
determines the value of r and thus the values in the coefficients matrix. The
following VBA code implements the Crank-Nicholson method. The partial
differential equation must be of the form shown in equation 12-29, that is,
a82C / 8x2 - 8C / t@ = 0 . The syntax of the function is CrankNichoIson(coet7,
delta-x, delta-f, prev-values). Coeff is the coefficient a in the above partial
differential equation. Delta-x is the size of the x-increment, which must be
constant. Delta-y is the size of the y-increment, which can vary. Prev-values is
the range of function values, including the endpoint values, in the preceding row.
The function returns an array of values in a row; the user must select the
appropriate range of cells for the results, then press CTRL+SHIFT+ENTER
(Windows) or CONTROL+SHIFT+RETURN (Macintosh) to enter the formula