Page 198 - Fair, Geyer, and Okun's Water and wastewater engineering : water supply and wastewater removal

JWCL344_ch05_154-193.qxd 8/2/10 9:44 PM Page 160

160 Chapter 5 Water Hydraulics, Transmission, and Appurtenances

VD VR
R
V 4 V
3 4 5 6
6 6 6 6
4 8 10 4 8 10 4 8 10 4 8 10
2 2 2 2
2 0.25
Rough
R f 1 D 0.15
2 log 1.14
D/k = 200 f k
3
D/k 20 4R/k 0.10
0.08
4
0.06
40 4
0.05
100
5 Laminar 0.04
8gRS 6 f 64 6 0.03
V 1 R f 200 8gRS V 2
400
0.025 Dh f /L
8g 7 k (ft) 1,000 0.020
C V 2 /2g
f
1 Boundary material 2,000 0.018 f
(new)
0.016
Glass; drawn brass, “Smooth”
8
4,000 8
copper, lead
Smooth
0.014
2 log R f 10,000
Wrought iron, steel 0.0001 − 0.0003 1
0.0002 − 0.0006 f 0.8
Asphalted cast iron
9
0.012
0.0002 − 0.0008 20,000
Galvanized iron
Cast iron 0.0004 − 0.002
7
Wood stave 0.0006 − 0.003
40,000
10
10
0.010
Concrete 0.0010 − 0.01 100,000
Riveted steel 0.0030 − 0.03
0.009
200,000
11
0.008
2 3 4 5
2 4 6 8 2 4 6 8 2 4 6 8 2 4 6 8
10 10 10 10
6
10
R f D v 3/2 2gh f 8R v 3/2 2gS
L
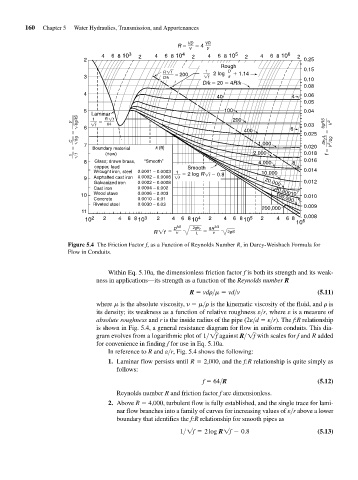
Figure 5.4 The Friction Factor f, as a Function of Reynolds Number R, in Darcy-Weisbach Formula for
Flow in Conduits.
Within Eq. 5.10a, the dimensionless friction factor f is both its strength and its weak-
ness in applications—its strength as a function of the Reynolds number R
R vd > vd>v (5.11)
where is the absolute viscosity, > is the kinematic viscosity of the fluid, and is
its density; its weakness as a function of relative roughness e>r, where e is a measure of
absolute roughness and r is the inside radius of the pipe (2e>d e>r). The f:R relationship
is shown in Fig. 5.4, a general resistance diagram for flow in uniform conduits. This dia-
gram evolves from a logarithmic plot of 1> 1f against R>1f with scales for f and R added
for convenience in finding f for use in Eq. 5.10a.
In reference to R and e>r, Fig. 5.4 shows the following:
1. Laminar flow persists until R 2,000, and the f:R relationship is quite simply as
follows:
f 64>R (5.12)
Reynolds number R and friction factor f are dimensionless.
2. Above R 4,000, turbulent flow is fully established, and the single trace for lami-
nar flow branches into a family of curves for increasing values of e>r above a lower
boundary that identifies the f:R relationship for smooth pipes as
1>1f = 2 log R1f - 0.8 (5.13)