Page 383 - Fiber Fracture

ATOMIC TRANSFORMATIONS 365

2.0
0.0

x -2.0
F
S -4.0
W
-6.0
-8.0

-1 0.0

-12.0
0 5 10 15 20 25
strain (%)
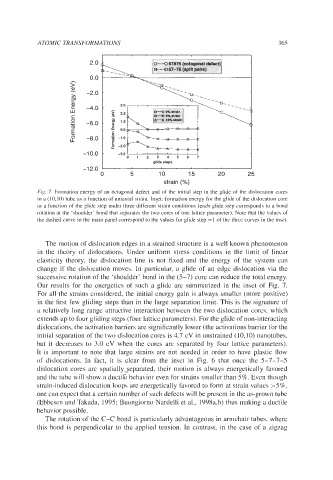
Ag 7. Formation energy of an octagonal defect and of the initial step in the glide of the dislocation cores
in a (10,lO) tube as a function of uniaxial strain. $et. formation energy for the glide of the dislocation core
as a function of the glide step under three different strain conditions (each glide step corresponds to a bond
rotation at the ‘shoulder’ bond that separates the two cores of one lattice parameter). Note that the values of
the dashed curve in the main panel correspond to the values for glide step =1 of the three curves in the inset.

The motion of dislocation edges in a strained structure is a well known phenomenon
in the theory of dislocations. Under uniform stress conditions in the limit of linear
elasticity theory, the dislocation line is not fixed and the energy of the system can
change if the dislocation moves. In particular, a glide of an edge dislocation via the
successive rotation of the ‘shoulder’ bond in the (5-7) core can reduce the total energy.
Our results for the energetics of such a glide are summarized in the inset of Fig. 7.
For all the strains considered, the initial energy gain is always smaller (more positive)
in the first few gliding steps than in the large separation limit. This is the signature of
a relatively long range attractive interaction between the two dislocation cores, which
extends up to four gliding steps (four lattice parameters). For the glide of non-interacting
dislocations, the activation barriers are significantly lower (the activations barrier for the
initial separation of the two dislocation cores is 4.7 eV in unstrained (10,lO) nanotubes,
but it decreases to 3.0 eV when the cores are separated by four lattice parameters).
It is important to note that large strains are not needed in order to have plastic flow
of dislocations. In fact, it is clear from the inset in Fig. 6 that once the 5-7-7-5
dislocation cores are spatially_separated, their motion is always energetically favored
and the tube will show a ductik behavior even for strains smaller than 5%. Even though
strain-induced dislocation loops are energetically favored to form at strain values >5%,
one can expect that a certain number of such defects will be present in the as-grown tube
(Ebbesen and Takada, 1995; Buongiorno Nardelli et al., 1998a,b) thus making a ductile
behavior possible.
The rotation of the C-C bond is particularly advantageous in armchair tubes, where
this bond is perpendicular to the applied tension. In contrast, in the case of a zigzag