Page 47 - Fiber Fracture

32 M. Elices and J. Llorca

.I DIAMETER (m)
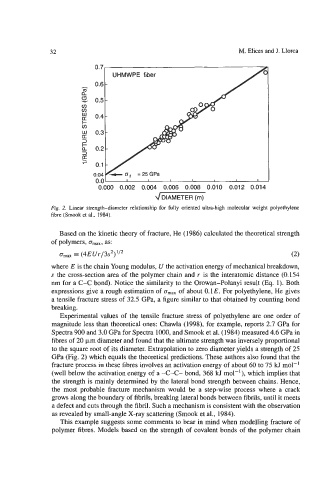
Fig. 2. Linear strength-diameter relationship for fully oriented ultra-high molecular weight polyethylene
fibre (Smook et ai., 1984).

Based on the kinetic theory of fracture, He (1 986) calculated the theoretical strength
of polymers, amax, as:
amax = (4EUr/3s2)”2 (2)
where E is the chain Young modulus, U the activation energy of mechanical breakdown,
s the cross-section area of the polymer chain and r is the interatomic distance (0.154
nm for a C-C bond). Notice the similarity to the Orowan-Polanyi result (Eq. 1). Both
expressions give a rough estimation of amax of about 0.1 E. For polyethylene, He gives
a tensile fracture stress of 32.5 GPa, a figure similar to that obtained by counting bond
breaking.
Experimental values of the tensile fracture stress of polyethylene are one order of
magnitude less than theoretical ones: Chawla (1998), for example, reports 2.7 GPa for
Spectra 900 and 3.0 GPa for Spectra 1000, and Smook et al. (1984) measured 4.6 GPa in
fibres of 20 wm diameter and found that the ultimate strength was inversely proportional
to the square root of its diameter. Extrapolation to zero diameter yields a strength of 25
GPa (Fig. 2) which equals the theoretical predictions. These authors also found that the
fracture process in these fibres involves an activation energy of about 60 to 75 kJ mol-’
(well below the activation energy of a -C-C- bond, 368 kJ mol-’), which implies that
the strength is mainly determined by the lateral bond strength between chains. Hence,
the most probable fracture mechanism would be a step-wise process where a crack
grows along the boundary of fibrils, breaking lateral bonds between fibrils, until it meets
a defect and cuts through the fibril. Such a mechanism is consistent with the observation
as revealed by small-angle X-ray scattering (Smook et al., 1984).
This example suggests some comments to bear in mind when modelling fracture of
polymer fibres. Models based on the strength of covalent bonds of the polymer chain