Page 50 - Fiber Fracture

MODELS OF FIBRE FRACTURE 35

8 7
- TORAYCAT30 HERCULES AS4
m
a
96-
+
I
0 1
2
W W Y
u 4- E (Gauge length 25.4 mm) 0-
[I) F L 3-
W TORAYCAM4 W
1
v) 2 2-
i5 2-
+ W
+
1-
I
ob I I I eI1,llL 0 d 2 4 6 8 10
I
DIAMETER ( p mm) GAUGE LENGTH (mm)
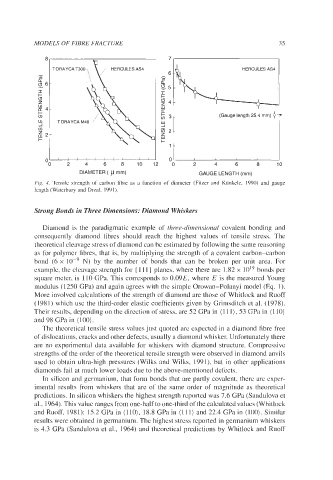
Fig. 4. Tensile strength of carbon fibre as a function of diameter (Fitzer and Kunkele, 1990) and gauge
length (Waterbury and Drzal, 1991).
Strong Bonds in Three Dimensions: Diamond Whiskers

Diamond is the paradigmatic example of three-dimensional covalent bonding and
consequently diamond fibres should reach the highest values of tensile stress. The
theoretical cleavage stress of diamond can be estimated by following the same reasoning
as for polymer fibres, that is, by multiplying the strength of a covalent carbon-carbon
bond (6 x lop9 N) by the number of bonds that can be broken per unit area. For
example, the cleavage strength for { 11 1 } planes, where there are 1.82 x lOI9 bonds per
square meter, is 110 GPa. This corresponds to 0.09E, where E is the measured Young
modulus (1250 GPa) and again agrees with the simple Orowan-Polanyi model (Eq. 1).
More involved calculations of the strength of diamond are those of Whitlock and Ruoff
(1981) which use the third-order elastic coefficients given by Grimsditch et al. (1978).
Their results, depending on the direction of stress, are 52 GPa in (1 1 l), 53 GPa in (1 10)
and 98 GPa in ( 100).
The theoretical tensile stress values just quoted are expected in a diamond fibre free
of dislocations, cracks and other defects, usually a diamond whisker. Unfortunately there
are no experimental data available for whiskers with diamond structure. Compressive
strengths of the order of the theoretical tensile strength were observed in diamond anvils
used to obtain ultra-high pressures (Wilks and Wilks, 1991), but in other applications
diamonds fail at much lower loads due to the above-mentioned defects.
In silicon and germanium, that form bonds that are partly covalent, there are exper-
imental results from whiskers that are of the same order of magnitude as theoretical
predictions. In silicon whiskers the highest strength reported was 7.6 GPa (Sandulova et
al., 1964). This value ranges from one-half to one-third of the calculated values (Whitlock
and Ruoff, 1981): 15.2 GPa in (1 lo), 18.8 GPa in (1 11) and 22.4 GPa in (100). Similar
results were obtained in germanium. The highest stress reported in germanium whiskers
is 4.3 GPa (Sandulova et al., 1964) and theoretical predictions by Whitlock and Ruoff