Page 55 - Fiber Fracture

40 M. Elices and J. Llorca

3.0

0.0

RELATIVE DEFECT SIZE, r / R
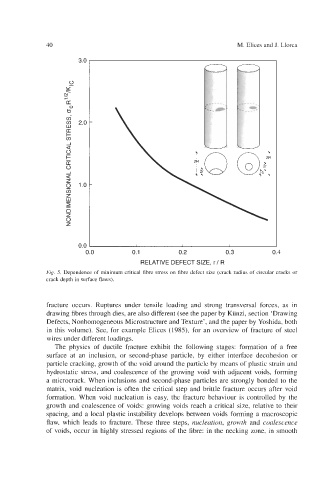
Fig. 5. Dependence of minimum critical fibre stress on fibre defect size (crack radius of circular cracks or
crack depth in surface flaws).

fracture occurs. Ruptures under tensile loading and strong transversal forces, as in
drawing fibres through dies, are also different (see the paper by Kunzi, section ‘Drawing
Defects, Nonhomogeneous Microstructure and Texture’, and the paper by Yoshida, both
in this volume). See, for example Elices (1985), for an overview of fracture of steel
wires under different loadings.
The physics of ductile fracture exhibit the following stages: formation of a free
surface at an inclusion, or second-phase particle, by either interface decohesion or
particle cracking, growth of the void around the particle by means of plastic strain and
hydrostatic stress, and coalescence of the growing void with adjacent voids, forming
a microcrack. When inclusions and second-phase particles are strongly bonded to the
matrix, void nucleation is often the critical step and brittle fracture occurs after void
formation. When void nucleation is easy, the fracture behaviour is controlled by the
growth and coalescence of voids: growing voids reach a critical size, relative to their
spacing, and a local plastic instability develops between voids forming a macroscopic
flaw, which leads to fracture. These three steps, nucleation, growth and coalescence
of voids, occur in highly stressed regions of the fibre: in the necking zone, in smooth