Page 127 - Finite Element Analysis with ANSYS Workbench

118 Chapter 7 Vibration Analysis

before using ANSYS software to solve an academic type problem.
Benefits of the method and software are demonstrated by analyzing
a practical application of an automobile frame structure.

7.1 Basic Equations

7.1.1 Differential Equations
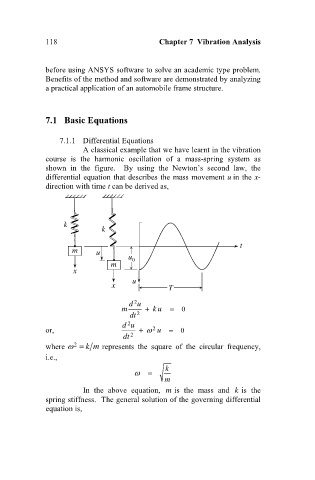
A classical example that we have learnt in the vibration
course is the harmonic oscillation of a mass-spring system as
shown in the figure. By using the Newton’s second law, the
differential equation that describes the mass movement u in the x-
direction with time t can be derived as,

k
k

t
m u
u
m 0
x
u
x T

2
m du  k u  0
dt 2
2
or, du   2 u  0
dt 2
where   km represents the square of the circular frequency,
2
i.e.,

k
 
m
In the above equation, m is the mass and k is the
spring stiffness. The general solution of the governing differential
equation is,