Page 123 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I 105

1.2

1 .o 0

0
2 0.8 0
s 0 8
.d
-
0.0
@ h 0.6 (b) 0’4/ 0.0 0.2 0.4 0.6 0.8 1.0
s
0.4
1.0,
0
0.2 5 - 0.81 0
0.0
0.0 0.2 0.4 0.6 0.8 P ......... 8 ................e
(a) UlU,,
Lo
0.0
0.0 0.2 0.4 0.6 0.8 0
(C) UIU,,

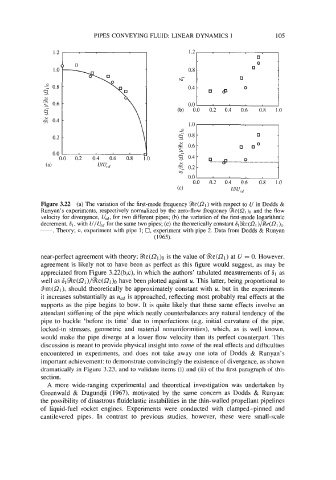
Figure 3.22 (a) The variation of the first-mode frequency %e(SZ1) with respect to U in Dodds &
Runyan’s experiments, respectively normalized by the zero-flow frequency %e(SZ, )o and the flow
velocity for divergence, U,, for two different pipes; (b) the variation of the first-mode logarithmic
decrement, 61, with U/Ucd for the same two pipes; (c) the theoretically constant 61%e(SZ,)/Re(L’nl )o.
-, Theory; 0, experiment with pipe 1; 0, experiment with pipe 2. Data from Dodds & Runyan
(1965).

near-perfect agreement with theory; %e(f21)o is the value of %e(fl1) at U = 0. However,
agreement is likely not to have been as perfect as this figure would suggest, as may be
appreciated from Figure 3.22(b,c), in which the authors’ tabulated measurements of 61 as
well as 6,%e(f21)/%e(f21)o have been plotted against u. This latter, being proportional to
.9m(D1), should theoretically be approximately constant with u, but in the experiments
it increases substantially as U,d is approached, reflecting most probably real effects at the
supports as the pipe begins to bow. It is quite likely that these same effects involve an
attendant stiffening of the pipe which neatly counterbalances any natural tendency of the
pipe to buckle ‘before its time’ due to imperfections (e.g. initial curvature of the pipe,
locked-in stresses, geometric and material nonunifonnities), which, as is well known,
would make the pipe diverge at a lower flow velocity than its perfect counterpart. This
discussion is meant to provide physical insight into some of the real effects and difficulties
encountered in experiments, and does not take away one iota of Dodds & Runyan’s
important achievement: to demonstrate convincingly the existence of divergence, as shown
dramatically in Figure 3.23, and to validate items (i) and (ii) of the first paragraph of this
section.
A more wide-ranging experimental and theoretical investigation was undertaken by
Greenwald & Dugundji (1967), motivated by the same concern as Dodds & Runyan:
the possibility of disastrous fluidelastic instabilities in the thin-walled propellant pipelines
of liquid-fuel rocket engines. Experiments were conducted with clamped-pinned and
cantilevered pipes. In contrast to previous studies, however, these were small-scale