Page 128 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

110 SLENDER STRUCTURES AND AXIAL FLOW

was discharged to atmosphere at the downstream end (collected and recirculated), and
axial sliding was permitted. Tension was applied via a pulley- weight mechanism. Typical
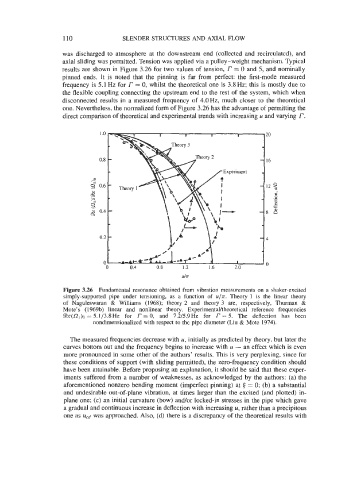
results are shown in Figure 3.26 for two values of tension, r = 0 and 5, and nominally
pinned ends. It is noted that the pinning is far from perfect: the first-mode measured
frequency is 5.1 Hz for r = 0, whilst the theoretical one is 3.8 Hz; this is mostly due to
the flexible coupling connecting the upstream end to the rest of the system, which when
disconnected results in a measured frequency of 4.0 Hz, much closer to the theoretical
one. Nevertheless, the normalized form of Figure 3.26 has the advantage of permitting the
direct comparison of theoretical and experimental trends with increasing u and varying r.

Figure 3.26 Fundamental resonance obtained from vibration measurements on a shaker-excited
simply-supported pipe under tensioning, as a function of u/n. Theory 1 is the linear theory
of Naguleswaran & Williams (1968); theory 2 and theory 3 are, respectively, Thurman &
Mote’s ( 1969b) linear and nonlinear theory. Experimentalltheoretical reference frequencies
Be(Ol)O = 5.1/3.8Hz for r = 0, and 7.215.9Hz for r = 5. The deflection has been
nondimensionalized with respect to the pipe diameter (Liu & Mote 1974).

The measured frequencies decrease with u, initially as predicted by theory, but later the
curves bottom out and the frequency begins to increase with u - an effect which is even
more pronounced in some other of the authors’ results. This is very perplexing, since for
these conditions of support (with sliding permitted), the zero-frequency condition should
have been attainable. Before proposing an explanation, it should be said that these exper-
iments suffered from a number of weaknesses, as acknowledged by the authors: (a) the
aforementioned nonzero bending moment (imperfect pinning) at e = 0; (b) a substantial
and undesirable out-of-plane vibration, at times larger than the excited (and plotted) in-
plane one; (c) an initial curvature (bow) and/or locked-in stresses in the pipe which gave
a gradual and continuous increase in deflection with increasing u, rather than a precipitous
one as u,d was approached. Also, (d) there is a discrepancy of the theoretical results with