Page 130 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

112 SLENDER STRUCTURES AND AXIAL FLOW

30

20

10
h
3
v
E
3
0
-IO

-20
0 20 40 60 80 100 120
(0)
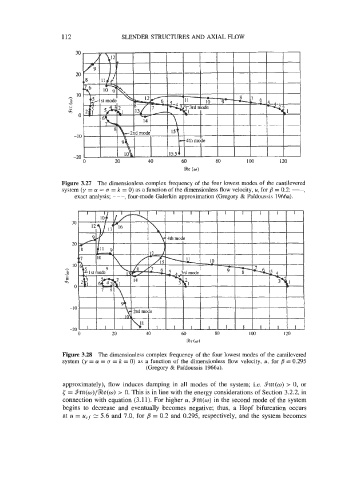
Figure 3.27 The dimensionless complex frequency of the four lowest modes of the cantilevered
system (y = ct = o = k = 0) as a function of the dimensionless flow velocity, u, for ,!? = 0.2: -,
exact analysis; - - -, four-mode Galerkin approximation (Gregory & Pafdoussis 1966a).

Figure 3.28 The dimensionless complex frequency of the four lowest modes of the cantilevered
system (y = ct = o = k = 0) as a function of the dimensionless flow velocity, u, for ,!? = 0.295
(Gregory & PaYdoussis 1966a).

approximately), flow induces damping in all modes of the system; i.e. $am(@) > 0, or
< = $m(w)/%e(o) > 0. This is in line with the energy considerations of Section 3.2.2, in
connection with equation (3.11). For higher u, 9m(w) in the second mode of the system
begins to decrease and eventually becomes negative; thus, a Hopf bifurcation occurs
at u = ucf 2: 5.6 and 7.0, for B = 0.2 and 0.295, respectively, and the system becomes