Page 135 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I 117

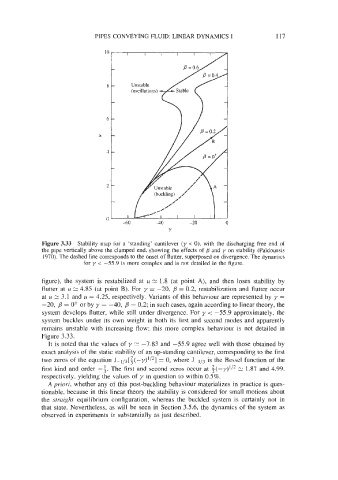
Figure 3.33 Stability map for a 'standing' cantilever (y < 0). with the discharging free end of
the pipe vertically above the clamped end, showing the effects of B and y on stability (Paidoussis
1970). The dashed line corresponds to the onset of flutter, superposed on divergence. The dynamics
for y < -55.9 is more complex and is not detailed in the figure.

figure), the system is restabilized at u E 1.8 (at point A), and then loses stability by
flutter at u 2 4.85 (at point B). For y = -20, = 0.2, restabilization and flutter occur
at u N 3.1 and u = 4.25, respectively. Variants of this behaviour are represented by y =
-20, p = O+ or by y = -40, = 0.2; in such cases, again according to linear theory, the
system develops flutter, while still under divergence. For y < -55.9 approximately, the
system buckles under its own weight in both its first and second modes and apparently
remains unstable with increasing flow: this more complex behaviour is not detailed in
Figure 3.33.
It is noted that the values of y 2 -7.83 and -55.9 agree well with those obtained by
exact analysis of the static stability of an up-standing cantilever, corresponding to the first
two zeros of the equation JL1/3[~(-y)1/2] = 0, where J-113 is the Bessel function of the
first kind and order -$. The first and second zeros occur at $(-y)'/* 2 1.87 and 4.99,
respectively. yielding the values of y in question to within 0.5%.
A priori. whether any of this post-buckling behaviour materializes in practice is ques-
tionable, because in this linear theory the stability is considered for small motions about
the straight equilibrium configuration, whereas the buckled system is certainly not in
that state. Nevertheless, as will be seen in Section 3.5.6, the dynamics of the system as
observed in experiments is substantially as just described.