Page 131 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I 113

unstable (in the linear sense) by flutter. For /I = 0.2, there is also a fourth-mode oscillatory
instability, via another Hopf bifurcation, at u 2 13.?
In the case of /l = 0.295 and for 7 < u < 8.2, the system loses stability, regains it and
loses it again, as the locus meanders along the %e(w)-axis. This cannot be seen very
clearly in the scale of Figure 3.28, but it is similar to what is easily visible in Figure 3.27
for 13 < u < 15 in the fourth mode.
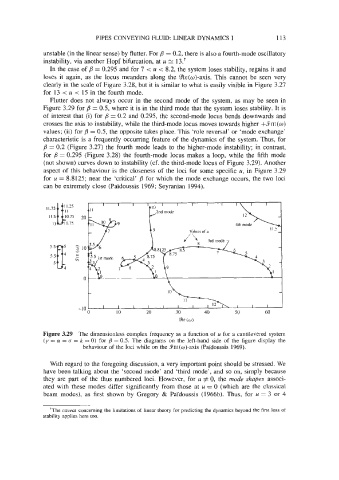
Flutter does not always occur in the second mode of the system, as may be seen in
Figure 3.29 for /l = 0.5, where it is in the third mode that the system loses stability. It is
of interest that (i) for B = 0.2 and 0.295, the second-mode locus bends downwards and
crosses the axis to instability, while the third-mode locus moves towards higher +4m(w)
values; (ii) for /I = 0.5, the opposite takes place. This ‘role reversal’ or ‘mode exchange’
characteristic is a frequently occurring feature of the dynamics of the system. Thus, for
/l = 0.2 (Figure 3.27) the fourth mode leads to the higher-mode instability; in contrast,
for = 0.295 (Figure 3.28) the fourth-mode locus makes a loop, while the fifth mode
(not shown) curves down to instability (cf. the third-mode locus of Figure 3.29). Another
aspect of this behaviour is the closeness of the loci for some specific u, in Figure 3.29
for u = 8.8125; near the ‘critical’ /I for which the mode exchange occurs, the two loci
11.75 k:.25
can be extremely close (Paidoussis 1969; Seyranian 1994).

11.5 10.75 20
I] 10.75

5.5

6,

0
- -
11
-10 I I I. I I 1 I I I I
0 10 20 30 40 50 60

Figure 3.29 The dimensionless complex frequency as a function of u for a cantilevered system
( y = a = cr = k = 0) for B = 0.5. The diagrams on the left-hand side of the figure display the
behaviour of the loci while on the Sm(o)-axis (Paidoussis 1969).

With regard to the foregoing discussion, a very important point should be stressed. We
have been talking about the ‘second mode’ and ‘third mode’, and so on, simply because
they are part of the thus numbered loci. However, for u # 0, the mode shapes associ-
ated with these modes differ significantly from those at u = 0 (which are the classical
beam modes), as first shown by Gregory & Paidoussis (1966b). Thus, for u = 3 or 4

‘The caveaf concerning the limitations of linear theory for predicting the dynamics beyond the first loss of
stability applies here too.