Page 134 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

116 SLENDER STRUCTURES AND AXIAL FLOW

flexible system may be considered as the limiting case of an articulated one as the number
of degrees of freedom N + 00, it is of interest to discover if divergence can arise in the
vertical continuous system as well.
Extensive calculations of Argand and stability diagrams for y # 0 were conducted by
Pdidoussis (1969, 1970), using the method of Section 3.3.6(b); it was found that N = 9
or 10 in the Galerkin series ensured accuracy of the eigenfrequencies to three significant
figures. Similar calculations were done by Bishop & Fawzy (1976).
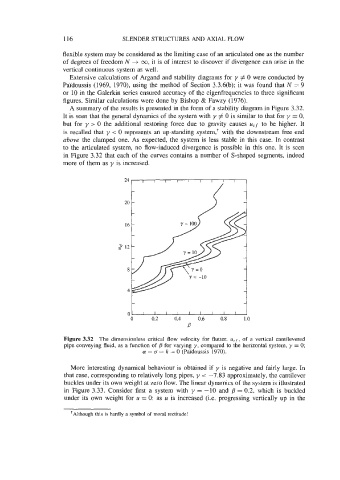
A summary of the results is presented in the form of a stability diagram in Figure 3.32.
It is seen that the general dynamics of the system with y # 0 is similar to that for y = 0,
but for y > 0 the additional restoring force due to gravity causes ucf to be higher. It
is recalled that y < 0 represents an up-standing system,+ with the downstream free end
above the clamped one. As expected, the system is less stable in this case. In contrast
to the articulated system, no flow-induced divergence is possible in this one. It is seen
in Figure 3.32 that each of the curves contains a number of S-shaped segments, indeed
more of them as y is increased.

0
0 0.2 0.4 0.6 0.8 1 .o
4

Figure 3.32 The dimensionless critical flow velocity for flutter, u,f, of a vertical cantilevered
pipe conveying fluid, as a function of fi for varying y, compared to the horizontal system, y = 0;
a = CJ = k = 0 (Pdidoussis 1970).

More interesting dynamical behaviour is obtained if y is negative and fairly large. In
that case, corresponding to relatively long pipes, y < -7.83 approximately, the cantilever
buckles under its own weight at zero flow. The linear dynamics of the system is illustrated
in Figure 3.33. Consider first a system with y = -10 and = 0.2, which is buckled
under its own weight for u = 0: as u is increased (Le. progressing vertically up in the

'Although this is hardly a symbol of moral rectitude!