Page 133 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I 115

0 0.2 0.4 0.6
B
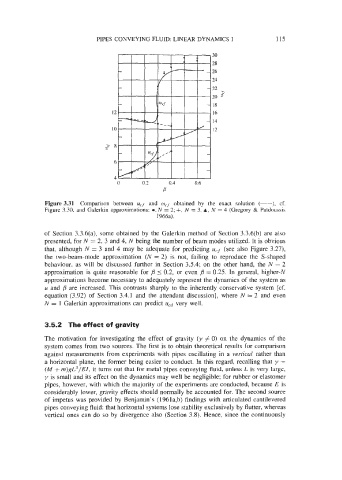
Figure 3.31 Comparison between urf and wCf obtained by the exact solution (-), cf.
Figure 3.30. and Galerkin approximations: 0, N = 2; +, N = 3, A, N = 4 (Gregory & Paidoussis
1966a).

of Section 3.3.6(a), some obtained by the Galerkin method of Section 3.3.6(b) are also
presented, for N = 2, 3 and 4, N being the number of beam modes utilized. It is obvious
that, although N = 3 and 4 may be adequate for predicting ucf (see also Figure 3.27),
the two-beam-mode approximation (N = 2) is not, failing to reproduce the S-shaped
behaviour, as will be discussed further in Section 3.5.4; on the other hand, the N = 2
approximation is quite reasonable for B 5 0.2, or even B = 0.25. In general, higher-N
approximations become necessary to adequately represent the dynamics of the system as
u and B are increased. This contrasts sharply to the inherently conservative system [cf.
equation (3.92) of Section 3.4.1 and the attendant discussion], where N = 2 and even
N = 1 Galerkin approximations can predict u,d very well.

3.5.2 The effect of gravity

The motivation for investigating the effect of gravity (y # 0) on the dynamics of the
system comes from two sources. The first is to obtain theoretical results for comparison
against measurements from experiments with pipes oscillating in a vertical rather than
a horizontal plane, the former being easier to conduct. In this regard, recalling that y =
(M + m)gL3/EZ, turns out that for metal pipes conveying fluid, unless L is very large,
it
y is small and its effect on the dynamics may well be negligible; for rubber or elastomer
pipes, however, with which the majority of the experiments are conducted, because E is
considerably lower, gravity effects should normally be accounted for. The second source
of impetus was provided by Benjamin’s (1961a,b) findings with articulated cantilevered
pipes conveying fluid: that horizontal systems lose stability exclusively by flutter, whereas
vertical ones can do so by divergence also (Section 3.8). Hence, since the continuously