Page 140 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

122 SLENDER STRUCTURES AND AXIAL FLOW

flutter, depending on the angle of the follower load to the last articulation and the ratio
of the viscous damping at the two articulations, and they display several other interesting
dynamical features. The destabilizing effect of vanishingly small damping as opposed to
zero damping can be so large as to reduce the critical load by a factor of more than 6!
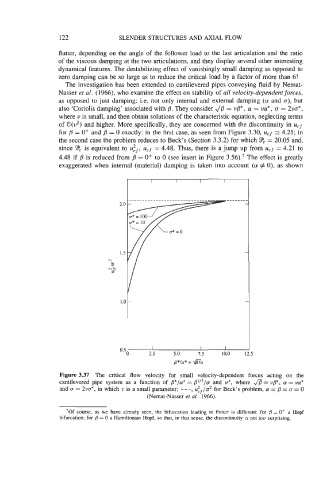
The investigation has been extended to cantilevered pipes conveying fluid by Nemat-
Nasser et al. (1966), who examine the effect on stability of all velocity-dependentforces,
as opposed to just damping: i.e. not only internal and external damping (a and a), but
also 'Coriolis damping' associated with #?. They consider z/B = up, a = ua*, a = 2uo*,
where u is small, and then obtain solutions of the characteristic equation, neglecting terms
of O(u2) and higher. More specifically, they are concerned with the discontinuity in ucf
for #? = O+ and #? = 0 exactly: in the first case, as seen from Figure 3.30, ucf 2: 4.21; in
the second case the problem reduces to Beck's (Section 3.3.2) for which '?Pc = 20.05 and,
since PC is equivalent to ucf = 4.48. Thus, there is a jump up from ucf = 4.21 to
4.48 if #? is reduced from #? = O+ to 0 (see insert in Figure 3.56).+ The effect is greatly
exaggerated when internal (material) damping is taken into account (a # 0), as shown

I I I I

2.0

1.5
-5
Nb
3

I .c

0.5
2.5 5.0 7.5 10.0 12.5
pva* = &CY
Figure 3.37 The critical flow velocity for small velocity-dependent forces acting on the
cantilevered pipe system as a function of /F/a!* = B'I2/cr and u*, where fl= up, a! = w*
and o = 2uo*, in which u is a small parameter; ---, u$/$ for Beck's problem, a! = B = o = 0
(Nemat-Nasser et al. 1966).

+Of course, as we have already seen, the bifurcation leading to flutter is different: for B = O+ a Hopf
bifurcation; for B = 0 a Hamiltonian Hopf, so that, in that sense, the discontinuity is not too surprising.