Page 144 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

126 SLENDER STRUCTURES AND AXIAL FLOW

0.4
0.2

dq 0.0
x
M
5 4.2
C
.- -
5
$j -0.4
m
-0.6
2
-0.8

: 0
0.005 0.010 0.015 0.020 0.025 0.030
(b) Damping coefficient, y2
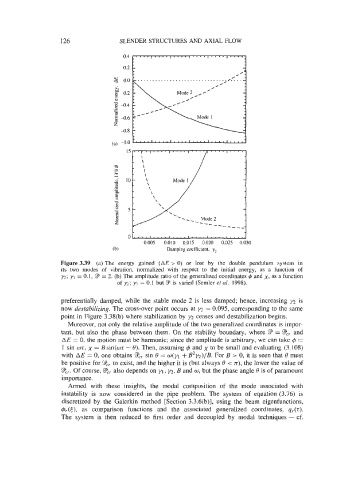
Figure 3.39 (a) The energy gained (AE > 0) or lost by the double pendulum system in
its two modes of vibration, normalized with respect to the initial energy, as a function of
y2; y1 = 0.1, 9 = 2. (b) The amplitude ratio of the generalized coordinates $ and x, as a function
of y2; yl = 0.1 but 9 is varied (Semler er al. 1998).

preferentially damped, while the stable mode 2 is less damped; hence, increasing y2 is
now destabilizing. The cross-over point occurs at y2 = 0.095, corresponding to the same
point in Figure 3.38(b) where stabilization by y2 ceases and destabilization begins.
Moreover, not only the relative amplitude of the two generalized coordinates is impor-
tant, but also the phase between them. On the stability boundary, where 9' = gCr and
AE = 0, the motion must be harmonic; since the amplitude is arbitrary, we can take q~ =
1 sin wt, x = Bsin(wt - 6). Then, assuming r$ and x to be small and evaluating (3.108)
with AE = 0, one obtains PCr sin 6 = w(yl + B2y2)/B. For B > 0, it is seen that 6 must
be positive for PCr to exist, and the higher it is (but always 6 < n), the lower the value of
Per. Of course, Pcr also depends on y1, y2, B and w, but the phase angle 6 is of paramount
importance.
Armed with these insights, the modal composition of the mode associated with
instability is now considered in the pipe problem. The system of equation (3.76) is
discretized by the Galerkin method [Section 3.3.6(b)], using the beam eigenfunctions,
4,. (Q, as comparison functions and the associated generalized coordinates, qr(r).
The system is then reduced to first order and decoupled by modal techniques - cf.