Page 143 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I 125

t
\
\
\ K P

0.000 0.005 0.010 0.015 0.020 0.025 0.030
(b) Damping coefficient, yz
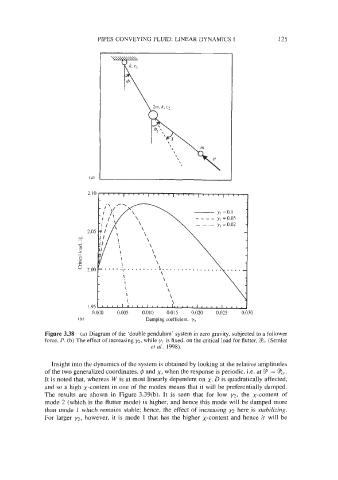
Figure 3.38 (a) Diagram of the 'double pendulum' system in zero gravity, subjected to a follower
force, P. (b) The effect of increasing M, while y~ is fixed, on the critical load for flutter. Y?,. (Semler
er nl. 1998).

Insight into the dynamics of the system is obtained by looking at the relative amplitudes
of the two generalized coordinates, 4 and x, when the response is periodic, i.e. at 9' = Per.
It is noted that, whereas W is at most linearly dependent on ,Y, D is quadratically affected,
and so a high X-content in one of the modes means that it will be preferentially damped.
The results are shown in Figure 3.39(b). It is seen that for low y2, the X-content of
mode 2 (which is the flutter mode) is higher, and hence this mode will be damped more
than mode 1 which remains stable: hence, the effect of increasing y2 here is stabilizing.
For larger y2, however, it is mode 1 that has the higher X-content and hence it will be