Page 145 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS 1 127

equations (2.16)-(2.19) - so that each eigenmode may be considered separately. It is
the modal content of the mode leading to flutter, in terms of the amplitudes GI and
the phases between them, that is of interest. Here the q,- are equivalent to and ,y in
the foregoing. The centrifugal term (a u') plays the role of 9, and Coriolis damping
(cx B'l'u) the role of the dissipative force due to y2.
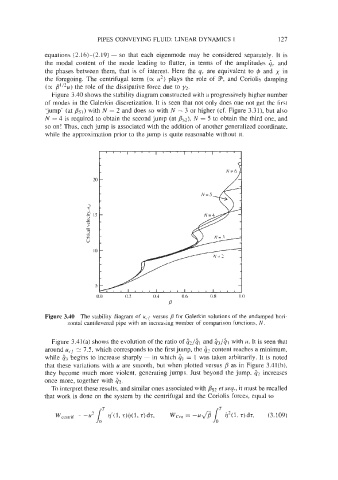
Figure 3.40 shows the stability diagram constructed with a progressively higher number
of modes in the Galerkin discretization. It is seen that not only does one not get the first
'jump' (at PSI) with N = 2 and does so with N = 3 or higher (cf. Figure 3.31), but also
N = 4 is required to obtain the second jump (at Bs~), = 5 to obtain the third one, and
N
so on! Thus, each jump is associated with the addition of another generalized coordinate,
while the approximation prior to the jump is quite reasonable without it.

P

Figure 3.40 The stability diagram of u,.f versus /3 for Galerkin solutions of the undamped hori-
zontal cantilevered pipe with an increasing number of comparison functions, N.

Figure 3.41(a) shows the evolution of the ratio of &/GI and 43/41 with u. It is seen that
around ii,f 2 7.5, which corresponds to the first jump, the 42 content reaches a minimum,
while @j begins to increase sharply - in which 41 = 1 was taken arbitrarily. It is noted
that these variations with u are smooth, but when plotted versus ,!3 as in Figure 3.41(b),
they become much more violent, generating jumps. Just beyond the jump. 42 increases
once more, together with 43.
et
To interpret these results, and similar ones associated with Bs~ seq., it must be recalled
that work is done on the system by the centrifugal and the Coriolis forces, equal lo