Page 210 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

192 SLENDER STRUCTURES AND AXIAL FLOW

The effect of some of the system parameters, e.g. the ratio of the stiffnesses and
the associated damping at the joints, and the ratio of masses of the two articulations is
investigated by Sugiyama & Paldoussis (1982), one aim being to find the configuration
leading to the minimum value of ucf.
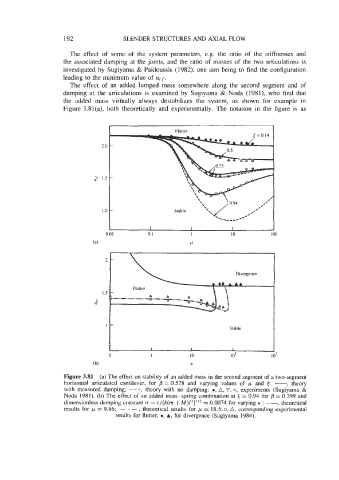
The effect of an added lumped mass somewhere along the second segment and of
damping at the articulations is examined by Sugiyama & Noda (1981), who find that
the added mass virtually always destabilizes the system, as shown for example in
Figure 3.81(a), both theoretically and experimentally. The notation in the figure is as

2.0

1.5

1 .o

I I I I
0.01 0.1 1 10 100
(a) CI

I-
Stable

L9 I I I

Figure 3.81 (a) The effect on stability of an added mass in the second segment of a two-segment
horizontal articulated cantilever, for B = 0.578 and varying values of p and 6: -, theory
with measured damping; ---, theory with no damping; e, A, 0, 0, experiments (Sugiyama &
Noda 1981). (b) The effect of an added mass-spring combination at e = 0.94 for fl = 0.299 and
dimensionless damping constant (T = c/[k(rn + M)13]'/2 = 0.0074 for varying K : -, theoretical
results for /1 = 9.86; - - - , theoretical results for p = 18.5; 0, A, corresponding experimental
results for flutter; 0, A, for divergence (Sugiyama 1984).