Page 249 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

230 SLENDER STRUCTURES AND AXIAL FLOW

is concerned, because the fluid discharging from the downstream end is assumed to
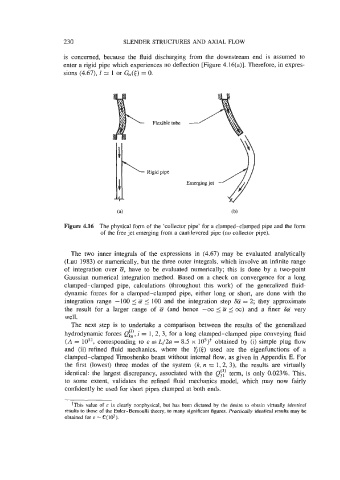
enter a rigid pipe which experiences no deflection [Figure 4.16(a)]. Therefore, in expres-
sions (4.67), I = 1 or Gn(.$) = 0.

Flexible tube

Rigid pipe

Figure 4.16 The physical form of the ‘collector pipe’ for a clamped-clamped pipe and the form
of the free jet emerging from a cantilevered pipe (no collector pipe).

The two inner integrals of the expressions in (4.67) may be evaluated analytically
(Luu 1983) or numerically, but the three outer integrals, which involve an infinite range
of integration over Z, have to be evaluated numerically; this is done by a two-point
Gaussian numerical integration method. Based on a check on convergence for a long
clamped-clamped pipe, calculations (throughout this work) of the generalized fluid-
dynamic forces for a clamped-clamped pipe, either long or short, are done with the
integration range -100 5 a! 5 100 and the integration step SZ = 2; they approximate
the result for a larger range of 5 (and hence -m 5 a! 5 m) and a finer 83 very
well.
The next step is to undertake a comparison between the results of the generalized
hydrodynamic forces Qfi, i = 1,2,3, for a long clamped-clamped pipe conveying fluid
(A = 1012, corresponding to E = L/2a = 8.5 x lo5)+ obtained by (i) simple plug flow
and (ii) refined fluid mechanics, where the $(t) used are the eigenfunctions of a
clamped-clamped Timoshenko beam without internal flow, as given in Appendix E. For
the first (lowest) three modes of the system (k, n = 1, 2,3), the results are virtually
identical: the largest discrepancy, associated with the Q:;) term, is only 0.023%. This,
to some extent, validates the refined fluid mechanics model, which may now fairly
confidently be used for short pipes clamped at both ends.

+This value of E is clearly nonphysical, but has been dictated by the desire to obtain virtually identical
results to those of the Euler-Bernoulli theory, to many significant figures. Pmctically identical results may be
obtained for E - S(l@).