Page 252 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I1 233

shear deformation is minimal; it approximates A + 00 very well. The effect of (T (rota-
tory inertia) has been shown to be negligible for realistic systems (Pdidoussis & Laithier
1976; Laithier 1979), and this is why the calculations have been conducted with o = 0.
The calculations are conducted according to the Timoshenko refined-flow (TRF), Timo-
shenko plug-flow (TPF) and the Euler-Bernoulli plug-flow (EBPF) theories and the results
compared.
For the TRF theory, for each length-to-diameter ratio E (and, correspondingly, for each
A), the work involved consists of (i) evaluating the generalized inviscid hydrodynamic
forces Qkn from (4.67); (ii) incorporating Qh into equations (4.44) to obtain the eigenfre-
quencies, and then (iii) constructing the corresponding Argand diagram of the system, to
obtain the critical velocity U& for divergence (the system being conservative; Section 3.4)
and the predicted post-divergence behaviour.
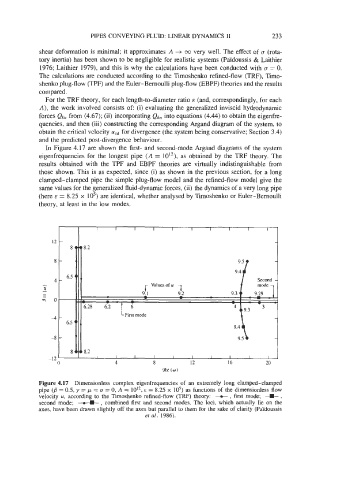
In Figure 4.17 are shown the first- and second-mode Argand diagrams of the system
eigenfrequencies for the longest pipe (A = 1OI2), as obtained by the TRF theory. The
results obtained with the TPF and EBPF theories are virtually indistinguishable from
those shown. This is as expected, since (i) as shown in the previous section, for a long
clamped-clamped pipe the simple plug-flow model and the refined-flow model give the
same values for the generalized fluid-dynamic forces, (ii) the dynamics of a very long pipe
(here E = 8.25 x lo5) are identical, whether analysed by Timoshenko or Euler-Bernoulli
theory, at least in the low modes.

Figure 4.17 Dimensionless complex eigenfrequencies of an extremely long clamped-clamped
pipe (p = 0.5, y = = CJ = 0, A = 10l2, E = 8.25 x lo5) as functions of the dimensionless flow
velocity u, according to the Timoshenko refined-flow (TRF) theory: e, mode; -,
first
,
second mode; 4 combined first and second modes. The loci, which actually lie on the
axes, have been drawn slightly off the axes but parallel to them for the sake of clarity (Pdidoussis
et al. 1986).