Page 256 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I1 237

Considering Figure 4.20 first, it is noticed that the eigenfrequencies as given by TRF
theory are higher than those obtained by TPF theory; the critical flow velocities for flutter
obtained by refined fluid mechanics (TRF theory) are also higher. These observations
are once again consistent with the concept of a smaller effective fluid mass per unit
length, M’, for the refined fluid mechanics, as compared to simple fluid mechanics. At the
same values of flow velocity and mode number, the absolute value of the eigenfrequency
obtained by the refined theory, Iurefl, is always larger than that obtained by the simple
theory, JwsimpI. Moreover, it is clear that M’ becomes increasingly smaller than M for
larger mode numbers (larger discrepancies in Figure 4.20); this is consistent with the fact
that M = pAf applies only if the wavelength of deformation is long, as compared to the
internal diameter of the pipe (Section 3.5.8) - which is not the case here for the second
and third modes. In this connection it is recalled (Section 3.5.1) that the modal shapes
for u > 0 contain components of higher zero-flow beam eigenfunctions, which reinforces
the foregoing argument.

I I I I I I I I I I I

- -

4, I I I I I I I I I I
0 4 8 12 16 20
9?c (w)

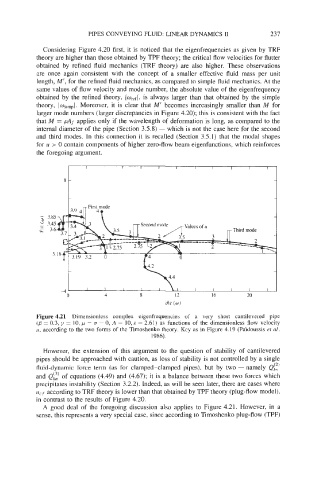
Figure 4.21 Dimensionlcss complex eigenfrequencies of a very short cantilevered pipe
(B = 0.3, y = 10. p = o = 0, A = 10, E = 2.61) as functions of the dimensionless flow velocity
11, according to the two forms of the Timoshenko theory. Key as in Figure 4.19 (Pai’doussis et nl.
1986).
However, the extension of this argument to the question of stability of cantilevered
pipes should be approached with caution, as loss of stability is not controlled by a single
fluid-dynamic force term (as for clamped-clamped pipes), but by two - namely QE,’
and QLi’ of equations (4.49) and (4.67); it is a balance between these two forces which
precipitates instability (Section 3.2.2). Indeed, as will be seen later, there are cases where
ucf according to TRF theory is lower than that obtained by TPF theory (plug-flow model).
in contrast to the results of Figure 4.20.
A good deal of the foregoing discussion also applies to Figure 4.21. However, in a
sense. this represents a very special case, since according to Timoshenko plug-flow (TPF)