Page 255 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

236 SLENDER STRUCTURES AND AXIAL FLOW

theory for A > lo3 approximately. On the other hand, for A < lo3, TPF theory tends to
underestimate u,d. The argument of end effects just discussed may be invoked here also to
explain these differences. The critical flow velocity for divergence depends principally on
the excitation force QE) - which in the plug-flow model is proportional to MU2; this is
smaller for refined fluid mechanics, since M' < M. Hence, this translates to uTy > uT;p".
For the EBPF theory the value of U,d is independent of A and equal to u:fpF = 6.66 (cf.
Figure 4.1 8), which is considerably higher than that obtained by the more appropriate
TRF and TPF theories for A < 1000 or so.

4.4.7 Stability of cantilevered pipes

Calculations for cantilevered pipes are conducted, utiiizing the outflow model developed
in Section 4.4.5(b), i.e. the 'second' or quadratic model with E = 2.8. In this case N =
7, 8 and 9 terms in the modal expansions (4.43) are necessary for convergence in the
first, second and third modes of the system, respectively. As in the previous section, the
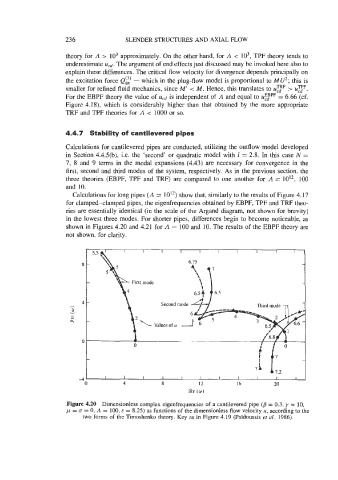
three theories (EBPF, TPF and TRF) are compared to one another for A = 100
and 10.
Calculations for long pipes (A = 10l2) show that, similarly to the results of Figure 4.17
for clamped-clamped pipes, the eigenfrequencies obtained by EBPF, TPF and TRF theo-
ries are essentially identical (in the scale of the Argand diagram, not shown for brevity)
in the lowest three modes. For shorter pipes, differences begin to become noticeable, as
shown in Figures 4.20 and 4.21 for A = 100 and 10. The results of the EBPF theory are
not shown, for clarity.

8

0

-4' I I I I I I I I I I I
0 4 8 12 16 20
%e (w)
Figure 4.20 Dimensionless complex eigenfrequencies of a cantilevered pipe (j3 = 0.3, y = 10,
p = 0 = 0, A = 100, E = 8.25) as functions of the dimensionless flow velocity u, according to the
two forms of the Timoshenko theory. Key as in Figure 4.19 (Pai'doussis et al. 1986).