Page 322 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)
P. 322
PIPES CONVEYING FLUID: NONLINEAR AND CHAOTIC DYNAMICS 303
I .oo
0.96
3 0.92
‘g
2
.- 0.88
3
.-
p 0.84
;a
.- -
E
E
0.80
0.76
0.72
0 I 2 3 4 5 6 7
Maximum tension increase/(EI/L*)
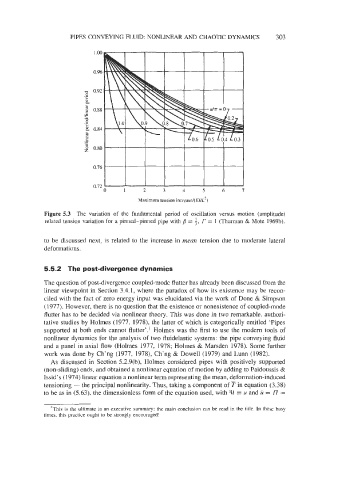
Figure 5.3 The variation of the fundamental period of oscillation versus motion (amplitude)
related tension variation for a pinned-pinned pipe with = i, f = 1 (Thurman & Mote 1969b).
to be discussed next, is related to the increase in mean tension due to moderate lateral
deformations.
5.5.2 The post-divergence dynamics
The question of post-divergence coupled-mode flutter has already been discussed from the
linear viewpoint in Section 3.4.1, where the paradox of how its existence may be recon-
ciled with the fact of zero energy input was elucidated via the work of Done & Simpson
( 1977). However, there is no question that the existence or nonexistence of coupled-mode
flutter has to be decided via nonlinear theory. This was done in two remarkable, authori-
tative studies by Holmes (1977, 1978), the latter of which is categorically entitled ‘Pipes
supported at both ends cannot flutter’.’ Holmes was the first to use the modern tools of
nonlinear dynamics for the analysis of two fluidelastic systems: the pipe conveying fluid
and a panel in axial flow (Holmes 1977, 1978; Holmes & Marsden 1978). Some further
work was done by Ch’ng (1977, 1978), Ch’ng & Dowel1 (1979) and Lunn (1982).
As discussed in Section 5.2.9(b), Holmes considered pipes with positively supported
(non-sliding) ends, and obtained a nonlinear equation of motion by adding to Pa1doussis &
Issid’s (1974) linear equation a nonlinear term representing the mean, deformation-induced
tensioning - the principal nonlinearity. Thus, taking a component of 7; in equation (3.38)
to be as in (5.63), the dimensionless form of the equation used, with Q = u and U = I7 =
+This is the ultimate in an executive summary: the main conclusion can be read in the title. In these busy
times, this practice ought to be strongly encouraged!