Page 332 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: NONLINEAR AND CHAOTIC DYNAMICS 313

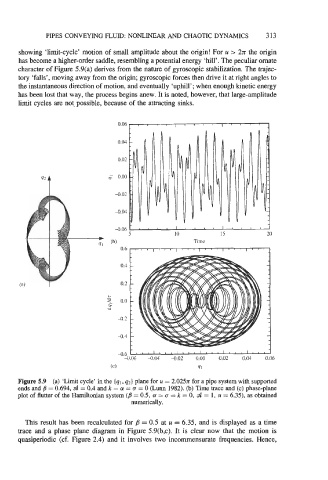
showing 'limit-cycle' motion of small amplitude about the origin! For u > 2n the origin
has become a higher-order saddle, resembling a potential energy 'hill'. The peculiar ornate
character of Figure 5.9(a) derives from the nature of gyroscopic stabilization. The trajec-
tory 'falls', moving away from the origin; gyroscopic forces then drive it at right angles to
the instantaneous direction of motion, and eventually 'uphill'; when enough kinetic energy
has been lost that way, the process begins anew. It is noted, however, that large-amplitude
limit cycles are not, possible, because of the attracting sinks.

0.04

0.02

q2 t 0.00

-0.02

-0.04

-0.6t' ' "' " ' " I " I "I I ""
I
-0.06 -0.04 -0.02 0.00 0.02 0.04 0.06
(C) 41
Figure 5.9 (a) 'Limit cycle' in the (ql, q2) plane for u = 2.025~ for a pipe system with supported
ends and /3 = 0.694, d = 0.4 and k = a, = = 0 (Lunn 1982). (b) Time trace and (c) phase-plane
plot of flutter of the Hamiltonian system (B = 0.5, (Y = (T = k = 0, d = 1, u = 6.35), as obtained
numerically.

This result has been recalculated for p = 0.5 at u = 6.35, and is displayed as a time
trace and a phase plane diagram in Figure 5.9(b,c). It is clear now that the motion is
quasiperiodic (cf. Figure 2.4) and it involves two incommensurate frequencies. Hence,