Page 341 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: NONLINEAR AND CHAOTIC DYNAMICS 321

An important result obtained by Rousselet & Henmdnn, with repercussions to most
other analyses, is that an amplitude of angular motion of at least 10" is required to
perturb the flow velocity by a few per cent. This justifies the assumption made in most
other analyses that the flow velocity is independent of motion.
Finally, in a qualitative experiment involving a system with 3 = 0.216, Rousselet &
Henmann found that the Hopf bifurcation is indeed subcritical: (i) for small disturbances,
the oscillations die out and the system returns to equilibrium, and (ii) for larger distur-
bances, the oscillations grow, until the motion reaches a steady state (stable limit cycle).
The same problem, but with joints of nonzero stiffness and simplified by considering
that the flow velocity is motion-independent, has been studied by Lunn (1982). In the
nonlinear equations, only cubic nonlinearities are retained. The dynamics in the vicinity
of the critical points is studied with the aid of centre manifold theory for both pitchfork
and Hopf bifurcations, in the latter case also making use of the multiple scales perturbation
technique (Nayfeh & Mook 1979; Nayfeh 1981).
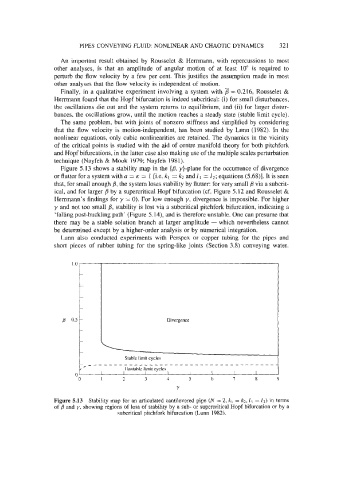
Figure 5.13 shows a stability map in the [j3, y}-plane for the occurrence of divergence
or flutter for a system with a = K = 1 [i.e. kl = k2 and 21 = 12; equations (5.68)j. It is seen
that, for small enough j3, the system loses stability by flutter: for very small B via a subcrit-
ical, and for larger /l by a supercritical Hopf bifurcation (cf. Figure 5.12 and Rousselet &
Hernnann's findings for y = 0). For low enough y, divergence is impossible. For higher
y and not too small 6, stability is lost via a subcritical pitchfork bifurcation, indicating a
'falling post-buckling path' (Figure 5.14), and is therefore unstable. One can presume that
there may be a stable solution branch at larger amplitude - which nevertheless cannot
be determined except by a higher-order analysis or by numerical integration.
Lunn also conducted experiments with Perspex or copper tubing for the pipes and
short pieces of rubber tubing for the spring-like joints (Section 3.8) conveying water.

1.0 \

\
Divergence

cycles
limit
Stabie
Unstable limit cycles
nl I I I I I
"
0 1 2 3 4 5 6 7 8 9
Y
Figure 5.13 Stability map for an articulated cantilevered pipe (N = 2, kl = k2,l L = 12) in terms
of B and y, showing regions of loss of stability by a sub- or supercritical Hopf bifurcation or by a
subcritical pitchfork bifurcation (Lunn 1982).