Page 432 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

7-
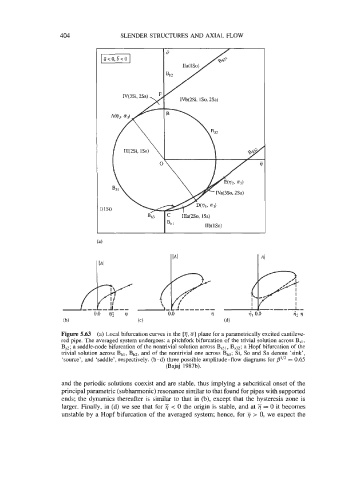
404 SLENDER STRUCTURES AND AXIAL FLOW
I Z<O,b<O I

IIa( 1 So)

IVb(2Si, ISo, 2Sa)

I(1Si)

IIb( 1 So)

Figure 5.63 (a) Local bifurcation curves in the (11, a) plane for a parametrically excited cantileve-
red pipe. The averaged system undergoes: a pitchfork bifurcation of the trivial solution across B,I,
Bs2; a saddle-node bifurcation of the nontrivial solution across Bs3,, Bs32; a Hopf bifurcation of the
trivial solution across Bhl, Bh2, and of the nontrivial one across Bh3; si, so and Sa denote ‘sink’,
‘source’, and ‘saddle’, respectively. (b-d) three possible amplitude-flow diagrams for = 0.65
(Bajaj 1987b).

and the periodic solutions coexist and are stable, thus implying a subcritical onset of the
principal parametric (subharmonic) resonance similar to that found for pipes with supported
ends; the dynamics thereafter is similar to that in (b), except that the hysteresis zone is
larger. Finally, in (d) we see that for 7 < 0 the origin is stable, and at ?j = 0 it becomes
unstable by a Hopf bifurcation of the averaged system; hence, for 11 > 0, we expect the