Page 427 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: NONLINEAR AND CHAOTIC DYNAMICS 399

0.50 /I

0.40 Damped
Undamped
0.30
P
0.20

0.10
II
(a) I 1
0.00 1 I I I If 1 I 1
3.00

2.00

I .00

0.00

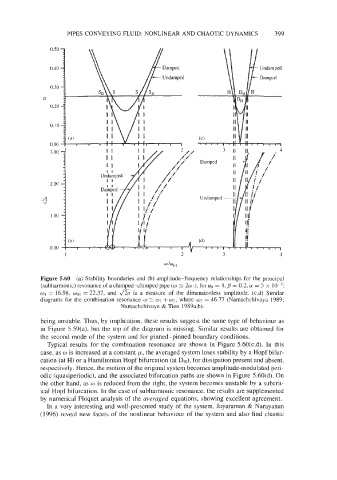
Figure 5.60 (a) Stability boundaries and (b) amplitude-frequency relationships for the principal
(subharmonic) resonance of a clamped-clamped pipe (w 2 2wl), for uo = 4, ,!I = 0.2, a = 5 x lo-':
is
wI = 16.98, wol = 22.37, and 6 measure of the dimensionless amplitude. (c,d) Similar
a
diagrams for the combination resonance w 2 wl + w2, where w2 = 46.77 (Namachchivaya 1989;
Namachchivaya & Tien 1989a,b).
being unstable. Thus, by implication, these results suggest the same type of behaviour as
in Figure 5.59(a), but the top of the diagram is missing. Similar results are obtained for
the second mode of the system and for pinned-pinned boundary conditions.
Typical results for the combination resonance are shown in Figure 5.60(c,d). In this
case, as u is increased at a constant p, the averaged system loses stability by a Hopf bifur-
cation (at H) or a Hamiltonian Hopf bifurcation (at DH), for dissipation present and absent,
respectively. Hence, the motion of the original system becomes amplitude-modulated peri-
odic (quasiperiodic), and the associated bifurcation paths are shown in Figure 5.60(d). On
the other hand, as w is reduced from the right, the system becomes unstable by a subcrit-
ical Hopf bifurcation. In the case of subharmonic resonance, the results are supplemented
by numerical Floquet analysis of the averaged equations, showing excellent agreement.
In a very interesting and well-presented study of the system, Jayaraman & Narayanan
(1996) reveal new facets of the nonlinear behaviour of the system and also find chaotic