Page 422 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)
P. 422
394 SLENDER STRUCTURES AND AXIAL FLOW
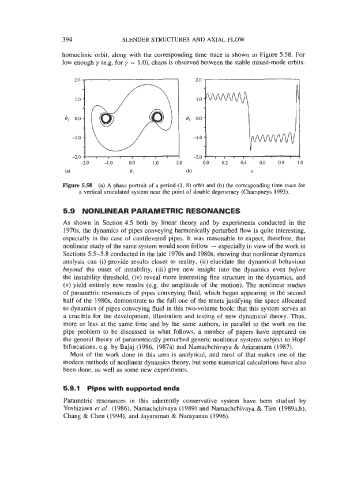
homoclinic orbit, along with the corresponding time trace is shown in Figure 5.58. For
low enough y (e.g. for y = 1 .O), chaos is observed between the stable mixed-mode orbits.
2.0 2.0
1.0 1.0 -
e, 0.0 6, 0.0 -
-1.0 -1.0 -
-2.0 -2.0- 1 I I I I 1 I I I
-2.0 -1.0 0.0 1 .o 2.0 0.0 0.2 0.4 0.6 0.8 1.0
(a) 4 (b) 7
Figure 5.58 (a) A phase portrait of a period-(1, 8) orbit and (b) the corresponding time trace for
a vertical articulated system near the point of double degeneracy (Champneys 1993).
5.9 NONLINEAR PARAMETRIC RESONANCES
As shown in Section 4.5 both by linear theory and by experiments conducted in the
1970s, the dynamics of pipes conveying harmonically perturbed flow is quite interesting,
especially in the case of cantilevered pipes. It was reasonable to expect, therefore, that
nonlinear study of the same system would soon follow - especially in view of the work in
Sections 5.5-5.8 conducted in the late 1970s and 1980s, showing that nonlinear dynamics
analysis can (i) provide results closer to reality, (ii) elucidate the dynamical behaviour
beyond the onset of instability, (iii) give new insight into the dynamics even before
the instability threshold, (iv) reveal more interesting fine structure in the dynamics, and
(v) yield entirely new results (e.g. the amplitude of the motion). The nonlinear studies
of parametric resonances of pipes conveying fluid, which began appearing in the second
half of the 1980s, demonstrate to the full one of the tenets justifying the space allocated
to dynamics of pipes conveying fluid in this two-volume book: that this system serves as
a crucible for the development, illustration and testing of new dynamical theory. Thus,
more or less at the same time and by the same authors, in parallel to the work on the
pipe problem to be discussed in what follows, a number of papers have appeared on
the general theory of parametrically perturbed generic nonlinear systems subject to Hopf
bifurcations, e.g. by Bajaj (1986, 1987a) and Namachchivaya & Ariaratnam (1987).
Most of the work done in this area is analytical, and most of that makes use of the
modem methods of nonlinear dynamics theory, but some numerical calculations have also
been done, as well as some new experiments.
5.9.1 Pipes with supported ends
Parametric resonances in this inherently conservative system have been studied by
Yoshizawa et al. (1986), Namachchivaya (1989) and Namachchivaya & Tien (1989a,b),
Chang & Chen (1994), and Jayaraman & Narayanan (1996).