Page 467 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

CURVED PIPES CONVEYING FLUID 439

the system with increasing U. Eight elements are adequate to obtain convergence in the
finite element scheme. At U = 0 the pipe behaves as a semi-circular ring (cf. Archer 1960;
Ojalvo 1962; Ojalvo & Newman 1965; Blevins 1979). As the flow velocity increases,
the eigenfrequencies become smaller according to this theory, and if the flow velocity
exceeds a certain value, the pipe becomes unstable by divergence in the first mode. With
further increase in the flow velocity, instability may occur in the higher modes, as well
as coupled-mode flutter (not shown). The results are qualitatively similar to those for a
straight pipe. It is noted that the finite element results obtained with the present analysis
agree very well with those obtained analytically by Chen (1972b). The same is also true
for clamped-pinned and pinned-pinned semi-circular pipes (Van 1986).
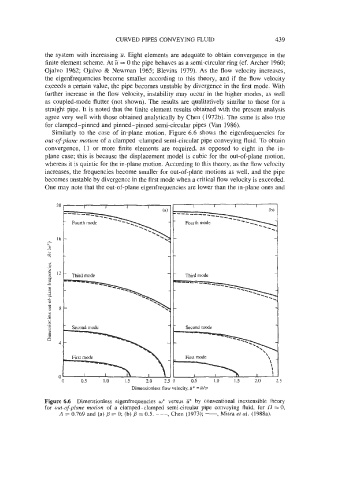
Similarly to the case of in-plane motion, Figure 6.6 shows the eigenfrequencies for
our-of-plane motion of a clamped-clamped semi-circular pipe conveying fluid. To obtain
convergence, 11 or more finite elements are required, as opposed to eight in the in-
plane case; this is because the displacement model is cubic for the out-of-plane motion,
whereas it is quintic for the in-plane motion. According to this theory, as the flow velocity
increases, the frequencies become smaller for out-of-plane motions as well, and the pipe
becomes unstable by divergence in the first mode when a critical flow velocity is exceeded.
One may note that the out-of-plane eigenfrequencies are lower than the in-plane ones and

Dimensionless flow velocity, E* = ii/~
Figure 6.6 Dimensionless eigenfrequencies w* versus U* by conventional inextensible theory
for out-of-phe motion of a clamped-clamped semi-circular pipe conveying fluid, for fl = 0,
A = 0.769 and (a) B = 0; (b) j5 = 0.5. ---, Chen (1973); -, Misra et nl. (19884.