Page 472 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

CURVED PIPES CONVEYING FLUID 443

Nevertheless, divergence according to this theory does not occur (as will be shown in
what follows); the global stiffness matrix remains positive definite.
For an inextensible pipe, there is no difference between the values of no for inviscid
and viscous flows; in both cases, it is equal to -ii*. For an extensible pipe, however,
there is a difference between viscous and inviscid results: small for low flow velocities,
but more significant at higher flows.
The dynamics of in-plane motion according to extensible theory is presented next.
Several variants of the theory are considered: in one, the steady-state combined force
no is neglected; in the second variant, no is taken into account, but the initial (steady)
deformations are assumed to be negligible, i.e. the terms involving d($’ + Oq;) in
equations (6.69) and (6.70) and (6.71) and (6.73) are set to zero;+ in the third variant both
no and d(rf + Oqi) are nonzero and it is considered to be the complete theory. The first
variant is recognized as physically not realizable, but is considered for comparison. The
calculations are conducted for a system with B = 0.5, dl = lo4 [see equations (6.46)J.
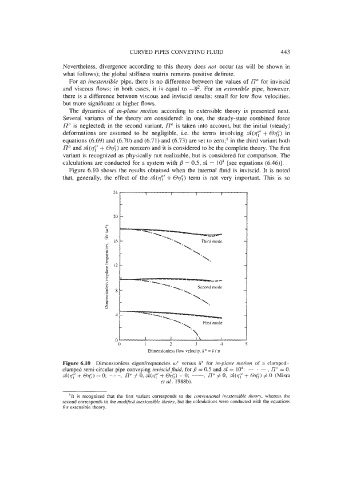
Figure 6.10 shows the results obtained when the internal fluid is inviscid. It is noted
that, generally, the effect of the d($’ + Or$) term is not very important. This is so

20

Dimensionless flow velocity. a* = ii/ P
Figure 6.10 Dimensionless eigenfrequencies w* versus P* for in-plane motion of a clamped-
clamped semi-circular pipe conveying inviscidfiuid, for fi = 0.5 and d = lo4: - . - , no = 0.
#
d(q:’ i- Oqt;) = 0; ---. IT” # 0. d(ie(rl7’ + @a;) = 0; --, l7“ # 0, d(rf + 0~;) (Misra
0
ef al. 1988b).
‘It is recognized that the first variant corresponds to the conveenfiond inextensible rheory, whereas the
second corresponds to the modified inextensible theory, but the calculations were conducted with the equations
for extensible theory.