Page 474 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

CURVED PIPES CONVEYING FLUID 445

Hill & Davis’ equations of motion are perhaps the closest to those utilized here, and
the results from these two theories are close, despite some parameters being different:
B = 0.43 and SQ = 1.4 x lo5 in Hill & Davis, as compared to 0.5 and lo4, respectively,
in the present case. Hill & Davis, similarly to the present theory, considered motions
about the deformed initial state calculated in a linearized fashion. On the other hand,
Doll & Mote calculated the deformed state by a more sophisticated approach, involving
a cumulative application of the linearized equations; their B is the same as in the present
calculations [note that this is so, despite what appears in their published work (#l = l),
due to a typographical error (Pdidoussis 1986b)l and d was 1.579 x lo4.
It should be noted that Doll & Mote and Hill & Davis effectively consider inviscid flow.
However, since the steady-state initial forces depend on real flow effects and these forces
do work in this case (unlike for straight pipes), this is not necessarily justified. Some
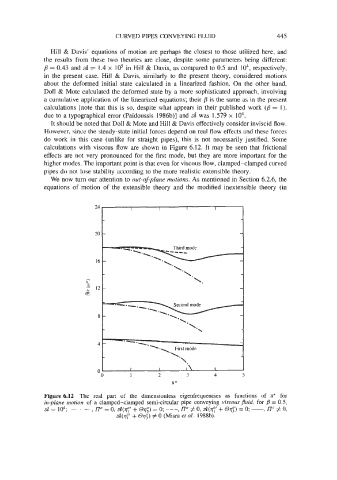
calculations with viscous flow are shown in Figure 6.12. It may be seen that frictional
effects are not very pronounced for the first mode, but they are more important for the
higher modes. The important point is that even for viscous flow, clamped-clamped curved
pipes do not lose stability according to the more realistic extensible theory.
We now turn our attention to out-ofplane motions. As mentioned in Section 6.2.6, the
equations of motion of the extensible theory and the modified inextensible theory (in

2oL
1

I
I
I
I\
I
0
0 1 2 3 4 5
a*
Figure 6.12 The real part of the dimensionless eigenfrequencies as functions of E* for
in-plane motion of a clamped-clamped semi-circular pipe conveying viscous Jluid, for B = 0.5,
se = 104; - . - , no = 0, se(vy’ + ev;) = 0; ---, no # 0, se(v~’ + ovp) = 0; -, no # 0,
d(rf + e$) # 0 (Misra et al. 1988b).