Page 478 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

CURVED PIPES CONVEYING FLUID 449

20

16
*
h
3
2
m-
.-
z
3 12
F
i
s
W
e
B
+
?
I 8
g
-
.n
n
C
.-
3
E
6
4
0
0 0.5 1 .o I .5 2.0 2.5
Dimensionless flow velocity, E*
-
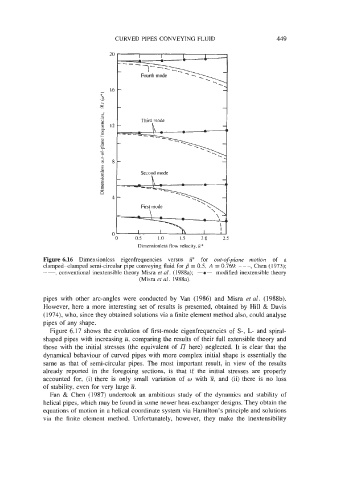
Figure 6.16 Dimensionless eigenfrequencies versus u* for out-of-plane motion of a
clamped-clamped semi-circular pipe conveying fluid for B = 0.5, A = 0.769: - --, Chen (1973);
-, conventional inextensible theory Misra et al. (1988a); -0- modified inextensible theory
(Misra et al. 1988a).

pipes with other arc-angles were conducted by Van (1986) and Misra etal. (1988b).
However, here a more interesting set of results is presented, obtained by Hill & Davis
(1974), who, since they obtained solutions via a finite element method also, could analyse
pipes of any shape.
Figure 6.17 shows the evolution of first-mode eigenfrequencies of S-, L- and spiral-
shaped pipes with increasing U, comparing the results of their full extensible theory and
those with the initial stresses (the equivalent of I7 here) neglected. It is clear that the
dynamical behaviour of curved pipes with more complex initial shape is essentially the
same as that of semi-circular pipes. The most important result, in view of the results
already reported in the foregoing sections, is that if the initial stresses are properly
accounted for, (i) there is only small variation of w with U, and (ii) there is no loss
of stability, even for very large E.
Fan & Chen (1987) undertook an ambitious study of the dynamics and stability of
helical pipes, which may be found in some newer heat-exchanger designs. They obtain the
equations of motion in a helical coordinate system via Hamilton’s principle and solutions
via the finite element method. Unfortunately, however, they make the inextensibility