Page 473 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

444 SLENDER STRUCTURES AND AXIAL FLOW

because the static deformations are not very large, as was observed earlier (Figure 6.9).
However, for U > 3n, static deformation effects become slightly more pronounced, in
the second and third modes particularly, reflecting relatively greater departures from the
unstressed state of the pipe.
The most important feature of Figure 6.10 is the fact that extensible theory, properly
taking into account the steady-state combined force no, predicts that no instability occurs
for a clamped-clamped curved pipe. The frequencies of the system change very slightly
with flow, unlike the case of no = 0 when the system is predicted to lose stability by
divergence. This leads to the conclusion that it is the steady flow-related forces, rather
than the steady deformations, which are primarily responsible for the inherent stability of
fluid-conveying clamped-clamped curved pipes, and this supports the basic tenet for the
modified inextensible theory, results for which are presented in Section 6.4.3.
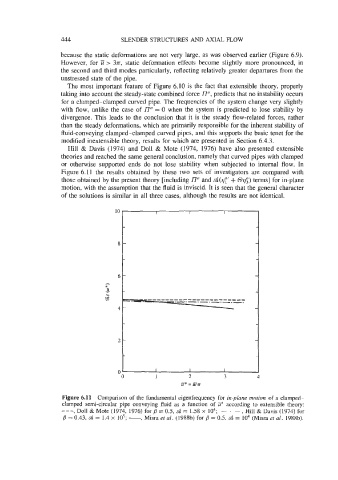
Hill & Davis (1974) and Doll & Mote (1974, 1976) have also presented extensible
theories and reached the same general conclusion, namely that curved pipes with clamped
or otherwise supported ends do not lose stability when subjected to internal flow. In
Figure 6.11 the results obtained by these two sets of investigators are compared with
those obtained by the present theory [including no and d(~p’ + 0~;) terms] for in-plane
motion, with the assumption that the fluid is inviscid. It is seen that the general character
of the solutions is similar in all three cases, although the results are not identical.

h
x
3

I I I I
0 1 2 3 4
ii* = EIP

Figure 6.11 Comparison of the fundamental eigenfrequency for in-plane motion of a clamped-
clamped semi-circular pipe conveying fluid as a function of 2 according to extensible theory:
_-_ , Doll & Mote (1974, 1976) for = 0.5, d = 1.58 x lo4; - . - , Hill & Davis (1974) for
j3 = 0.43, d = 1.4 x lo5; - Misra et al. (1988b) for B = 0.5, d = lo4 (Misra et al. 1988b).
,