Page 479 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

-- -

I I I I 1 I I I 1 I

--- + -
so -- - --.
In-plane 70 -\ -z
i.

6 8 10
ii

I I I I I I I
260 -
In-plane --- ---I_
250 0 nP = 0 & 40.12
E
3

0 2 4 6 8 101214
ii
(C)
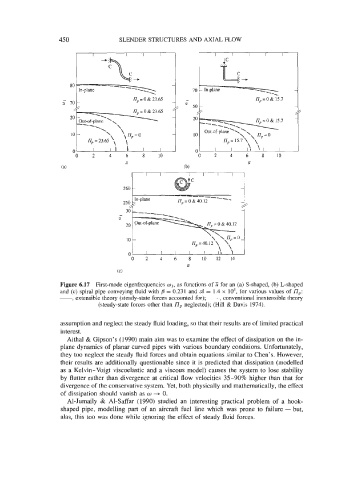
Figure 6.17 First-mode eigenfrequencies w1, as functions of U for an (a) S-shaped, (b) L-shaped
and (c) spiral pipe conveying fluid with = 0.231 and d = 1.4 x lo5, for various values of nP:
-, extensible theory (steady-state forces accounted for); - - -, conventional inextensible theory
(steady-state forces other than 17, neglected); (Hill & Davis 1974).

assumption and neglect the steady fluid loading, so that their results are of limited practical
interest.
Aithal & Gipson's (1990) main aim was to examine the effect of dissipation on the in-
plane dynamics of planar curved pipes with various boundary conditions. Unfortunately,
they too neglect the steady fluid forces and obtain equations similar to Chen's. However,
their results are additionally questionable since it is predicted that dissipation (modelled
as a Kelvin-Voigt viscoelastic and a viscous model) causes the system to lose stability
by flutter rather than divergence at critical flow velocities 35-90% higher than that for
divergence of the conservative system. Yet, both physically and mathematically, the effect
of dissipation should vanish as w -+ 0.
Al-Jumaily & Al-Saffar (1990) studied an interesting practical problem of a hook-
shaped pipe, modelling part of an aircraft fuel line which was prone to failure - but,
alas, this too was done while ignoring the effect of steady fluid forces.