Page 66 - Instant notes

Physical Chemistry 52

The system entropy change for an irreversible process is unchanged compared to that for
a reversible process as entropy is a state function. The entropy change of the
surroundings is always −dq/dT. Thus the total entropy change is zero for a reversible
process and >0 for an irreversible process. This is the second law of thermodynamics
(see Topic B5).
It is possible to measure the system entropy changes by measuring the heat capacity,
C, as a function of temperature. If heat is added reversibly to a system, dq rev=CdT and
dS=CdT/T, and the entropy change is then given by:

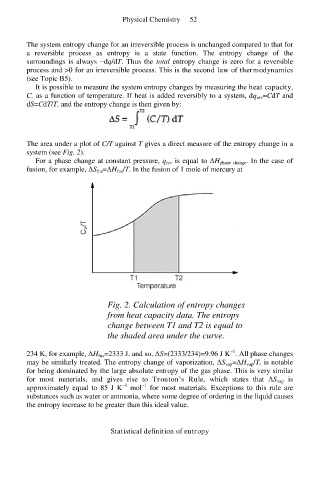
The area under a plot of C/T against T gives a direct measure of the entropy change in a
system (see Fig. 2).
For a phase change at constant pressure, q rev is equal to ∆H phase change. In the case of
fusion, for example, ∆S fus=∆H fus/T. In the fusion of 1 mole of mercury at

Fig. 2. Calculation of entropy changes
from heat capacity data. The entropy
change between T1 and T2 is equal to
the shaded area under the curve.

−1
234 K, for example, ∆H fus=2333 J, and so, ∆S=(2333/234)=9.96 J K . All phase changes
may be similarly treated. The entropy change of vaporization, ∆S vap=∆H vap/T, is notable
for being dominated by the large absolute entropy of the gas phase. This is very similar
for most materials, and gives rise to Trouton’s Rule, which states that ∆S vap is
−1
−1
approximately equal to 85 J K mol for most materials. Exceptions to this rule are
substances such as water or ammonia, where some degree of ordering in the liquid causes
the entropy increase to be greater than this ideal value.

Statistical definition of entropy