Page 121 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I 103

The first equation is associated with n = 1; the second with n 2 2, such that n is the
smallest integer satisfying

n4 + 2n3 + 3n2 + 2n + 6 1 k/n4, (3.104)

e.g. n = 2 if 8411 1 5 k/n4 5 54, n = 3 if 54 5 k/n4 5 174, n = 4 if 174 5 k/n4 5 446,
etc. Equations (3.102) and (3.104) differ from the criteria given by Roth, which can lead
to a nonconservative value of Vcd. The Galerkin solutions (3.103) were compared to an
exact solution and found always to overestimate the exact vcd, but by less than 2%.
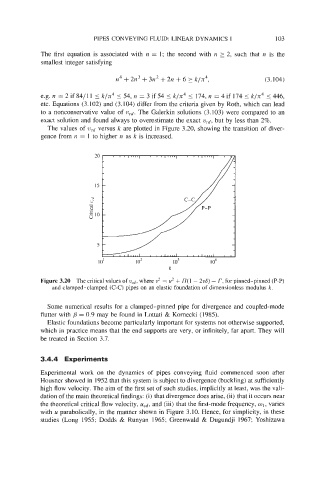
The values of 2& versus k are plotted in Figure 3.20, showing the transition of diver-
gence from n = 1 to higher n as k is increased.

20

15

5

10' I o3
k
Figure 3.20 The critical values of ucdr where u2 = u2 + n(1 - 2uS) - r, for pinned-pinned (P-P)
and clamped-clamped (C-C) pipes on an elastic foundation of dimensionless modulus k.

Some numerical results for a clamped-pinned pipe for divergence and coupled-mode
flutter with /3 = 0.9 may be found in Lottati & Kornecki (1985).
Elastic foundations become particularly important for systems not otherwise supported,
which in practice means that the end supports are very, or infinitely, far apart. They will
be treated in Section 3.7.

3.4.4 Experiments
Experimental work on the dynamics of pipes conveying fluid commenced soon after
Housner showed in 1952 that this system is subject to divergence (buckling) at sufficiently
high flow velocity. The aim of the first set of such studies, implicitly at least, was the vali-
dation of the main theoretical findings: (i) that divergence does arise, (ii) that it occurs near
the theoretical critical flow velocity, ucd, and (iii) that the first-mode frequency, w1, varies
with u parabolically, in the manner shown in Figure 3.10. Hence, for simplicity, in these
studies (Long 1955; Dodds & Runyan 1965; Greenwald & Dugundji 1967; Yoshizawa