Page 146 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

128 SLENDER STRUCTURES AND AXIAL FLOW

0.7
--a=O
0.6 E - - a = 0.01
0.5
Q
*
.*
&
$ 0.4
m
Q
.8 - 0.3
E c 4
z" 0.2
0.1
0.0
5 6 7 8 9 10
(a) Critical flow velocity, ud
0.7

0.6
* 0.5
9
.- -
$ 0.4
m
-e
.3 - 0.3
E
z" 0.2
0.1
0.0
0.2 0.4 0.6 0.8
(b) Mass parameter, B

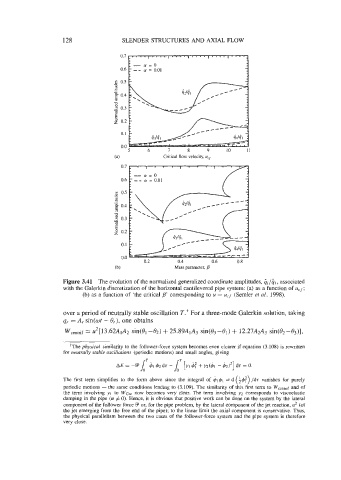
Figure 3.41 The evolution of the normalized generalized coordinate amplitudes, Gi/G,, associated
with the Galerkin discretization of the horizontal cantilevered pipe system: (a) as a function of uti;
(b) as a function of 'the critical p' corresponding to u = uCf (Semler et al. 1998).

over a period of neutrally stable oscillation T.+ For a three-mode Galerkin solution, taking
q, = A, sintot - &), one obtains
Wcentrif = u2[13.62A1A2 sin(81-02) + 25.89AlA3 sin(& -0,) + 12.27A2A3 ~in(0~-&)],

?The physical similarity to the follower-force system becomes even clearer if equation (3.108) is rewritten
for neutrally stable oscillations (periodic motions) and small angles, giving

The first term simplifies to the form above since the integral of &q$ 3 d (i4:) /dt vanishes for purely
periodic motions - the same conditions leading to (3.109). The similarity of this first term to Wcentrif and of
the term involving yi to Wcor now becomes very clear. The term involving yz corresponds to viscoelastic
damping in the pipe (a # 0). Hence, it is obvious that positive work can be done on the system by the lateral
component of the follower force 9 or, for the pipe problem, by the lateral component of the jet reaction, u2 (of
the jet emerging from the free end of the pipe); to the linear limit the axial component is conservative. Thus,
the physical parallelism between the two cases of the follower-force system and the pipe system is therefore
very close.