Page 150 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

132 SLENDER STRUCTURES AND AXIAL FLOW

0.0 0.2 0.4 0.6 0.8 1 .o
P
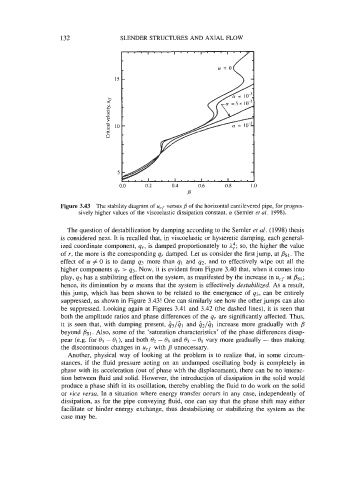
Figure 3.43 The stability diagram of ucf versus ,9 of the horizontal cantilevered pipe, for progres-
sively higher values of the viscoelastic dissipation constant, a! (Semler et al. 1998).

The question of destabilization by damping according to the Semler et al. (1998) thesis
is considered next. It is recalled that, in viscoelastic or hysteretic damping, each general-
ized coordinate component, qr, is damped proportionately to A:; so, the higher the value
of r, the more is the corresponding qr damped. Let us consider the first jump, at PSI. The
effect of (11 # 0 is to damp q3 more than q1 and q2, and to effectively wipe out all the
higher components qr > q3. Now, it is evident from Figure 3.40 that, when it comes into
play, q3 has a stabilizing effect on the system, as manifested by the increase in ucf at PSI;
hence, its diminution by a! means that the system is effectively destabilized. As a result,
this jump, which has been shown to be related to the emergence of 43, can be entirely
suppressed, as shown in Figure 3.43! One can similarly see how the other jumps can also
be suppressed. Looking again at Figures 3.41 and 3.42 (the dashed lines), it is seen that
both the amplitude ratios and phase differences of the qr are significantly affected. Thus,
it is seen that, with damping present, 43/41 and 42/41 increase more gradually with P
beyond PSI. Also, some of the ‘saturation characteristics’ of the phase differences disap-
pear (e.g. for 0, - el), and both 02 - 03 and 0, - 01 vary more gradually - thus making
the discontinuous changes in ucf with unnecessary.
Another, physical way of looking at the problem is to realize that, in some circum-
stances, if the fluid pressure acting on an undamped oscillating body is completely in
phase with its acceleration (out of phase with the displacement), there can be no interac-
tion between fluid and solid. However, the introduction of dissipation in the solid would
produce a phase shift in its oscillation, thereby enabling the fluid to do work on the solid
or vice versa. In a situation where energy transfer occurs in any case, independently of
dissipation, as for the pipe conveying fluid, one can say that the phase shift may either
facilitate or hinder energy exchange, thus destabilizing or stabilizing the system as the
case may be.