Page 253 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)
P. 253
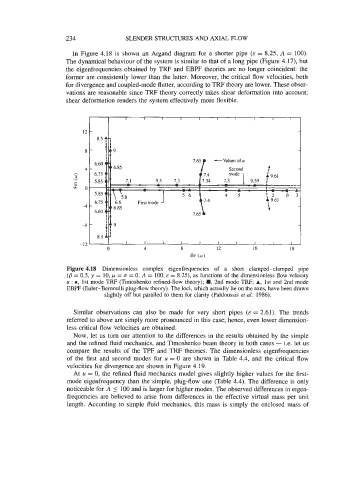
234 SLENDER STRUCTURES AND AXIAL FLOW
In Figure 4.18 is shown an Argand diagram for a shorter pipe (E = 8.25, A = 100).
The dynamical behaviour of the system is similar to that of a long pipe (Figure 4.17), but
the eigenfrequencies obtained by TRF and EBPF theories are no longer coincident: the
former are consistently lower than the latter. Moreover, the critical flow velocities, both
for divergence and coupled-mode flutter, according to TRF theory are lower. These obser-
vations are reasonable since TRF theory correctly takes shear deformation into account;
shear deformation renders the system effectively more flexible.
I I 1 I I I I 1 I I
12 - -
8.5 f;
II
8- I t9 -
ir
6.60 e-
4- 4 1 6.85 I A -
9.61
9.59 I ---
-
a 1 . ..--A-
0 3
\ 261
* -
\
I A
-8 - 9 -
'I
8.5 1
-12 I I I I I I I I I I
0 4 8 12 16 18
Figure 4.18 Dimensionless complex eigenfrequencies of a short clamped-clamped pipe
(B = 0.5, y = 10, p = u = 0; A = 100, E = 8.25), as functions of the dimensionless flow velocity
u : 0, 1st mode TRF (Timoshenko refined-flow theory); W, 2nd mode TRF; A, 1st and 2nd mode
EBPF (Euler-Bernoulli plug-flow theory). The loci, which actually lie on the axes, have been drawn
slightly off but paralled to them for clarity (Pafdoussis et al. 1986).
Similar observations can also be made for very short pipes (E = 2.61). The trends
referred to above are simply more pronounced in this case; hence, even lower dimension-
less critical flow velocities are obtained.
Now, let us turn our attention to the differences in the results obtained by the simple
and the refined fluid mechanics, and Timoshenko beam theory in both cases - i.e. let us
compare the results of the TPF and TRF theories. The dimensionless eigenfrequencies
of the first and second modes for u = 0 are shown in Table 4.4, and the critical flow
velocities for divergence are shown in Figure 4.19.
At u = 0, the refined fluid mechanics model gives slightly higher values for the first-
mode eigenfrequency than the simple, plug-flow one (Table 4.4). The difference is only
noticeable for A 5 100 and is larger for higher modes. The observed differences in eigen-
frequencies are believed to arise from differences in the effective virtual mass per unit
length. According to simple fluid mechanics, this mass is simply the enclosed mass of