Page 196 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C004.fm Page 176 Thursday, April 21, 2005 5:38 PM

176 Fracture Mechanics: Fundamentals and Applications

The advantage of Equation (4.2) is that the displacement and displacement rate can be measured
experimentally. The transition time is defined at the moment in the test when the ratio E /U = 1. In
k
order to obtain an explicit expression for t , it is convenient to introduce a dimensionless displacement
τ
coefficient D:
tt ()∆
˙
D = (4.4)
∆ t ()
t τ
If, for example, the displacement varies with time as a power law: ∆ = βtγ, then D = γ . Combining
Equation (4.2) and Equation (4.4) and setting E /U = 1 leads to
k
W
t τ D = Λ c o (4.5)

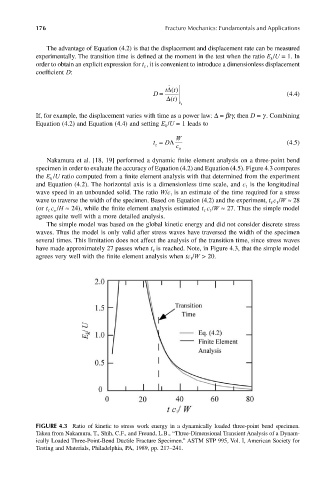
Nakamura et al. [18, 19] performed a dynamic finite element analysis on a three-point bend
specimen in order to evaluate the accuracy of Equation (4.2) and Equation (4.5). Figure 4.3 compares
the E /U ratio computed from a finite element analysis with that determined from the experiment
k
and Equation (4.2). The horizontal axis is a dimensionless time scale, and c is the longitudinal
1
wave speed in an unbounded solid. The ratio W/c is an estimate of the time required for a stress
1
wave to traverse the width of the specimen. Based on Equation (4.2) and the experiment, t c /W ≈ 28
τ 1
(or t c /H ≈ 24), while the finite element analysis estimated t c /W ≈ 27. Thus the simple model
τ o
τ 1
agrees quite well with a more detailed analysis.
The simple model was based on the global kinetic energy and did not consider discrete stress
waves. Thus the model is only valid after stress waves have traversed the width of the specimen
several times. This limitation does not affect the analysis of the transition time, since stress waves
have made approximately 27 passes when t is reached. Note, in Figure 4.3, that the simple model
τ
agrees very well with the finite element analysis when tc /W > 20.
1

FIGURE 4.3 Ratio of kinetic to stress work energy in a dynamically loaded three-point bend specimen.
Taken from Nakamura, T., Shih, C.F., and Freund, L.B., “Three-Dimensional Transient Analysis of a Dynam-
ically Loaded Three-Point-Bend Ductile Fracture Specimen.” ASTM STP 995, Vol. I, American Society for
Testing and Materials, Philadelphia, PA, 1989, pp. 217–241.