Page 197 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C004.fm Page 177 Thursday, April 21, 2005 5:38 PM

Dynamic and Time-Dependent Fracture 177

When t >> t , inertia effects are negligible and quasistatic models should apply to the problem.
τ
Consequently, the J integral for a deeply cracked bend specimen at long times can be estimated
by

∗
2
Ω
t
J = Bb ∫ 0 Ω t () Mt d () (4.6)
()
dc
where
B = plate thickness
b = uncracked ligament length
M = applied moment on the ligament
Ω = angle of rotation
t* = current time

Equation (4.6), which was originally published by Rice et al. [20], is derived in Section 3.2.5.
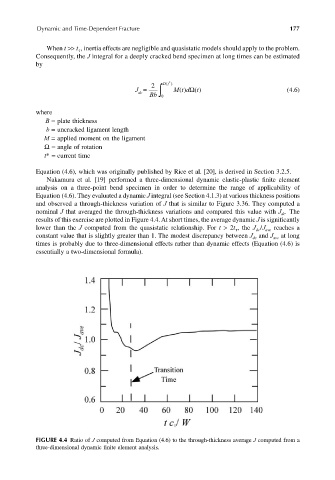
Nakamura et al. [19] performed a three-dimensional dynamic elastic-plastic finite element
analysis on a three-point bend specimen in order to determine the range of applicability of
Equation (4.6). They evaluated a dynamic J integral (see Section 4.1.3) at various thickness positions
and observed a through-thickness variation of J that is similar to Figure 3.36. They computed a
nominal J that averaged the through-thickness variations and compared this value with J . The
dc
results of this exercise are plotted in Figure 4.4. At short times, the average dynamic J is significantly
lower than the J computed from the quasistatic relationship. For t > 2t , the J /J reaches a
τ
dc
ave
constant value that is slightly greater than 1. The modest discrepancy between J and J at long
dc
ave
times is probably due to three-dimensional effects rather than dynamic effects (Equation (4.6) is
essentially a two-dimensional formula).

FIGURE 4.4 Ratio of J computed from Equation (4.6) to the through-thickness average J computed from a
three-dimensional dynamic finite element analysis.