Page 261 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C005.fm Page 241 Monday, May 23, 2005 5:47 PM

Fracture Mechanisms in Metals 241

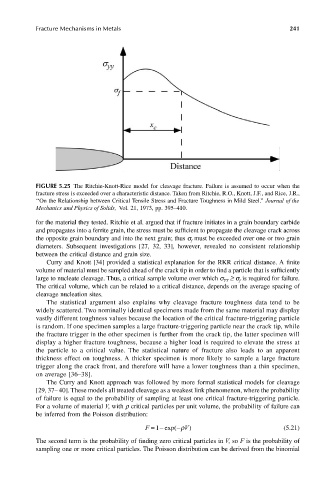
FIGURE 5.25 The Ritchie-Knott-Rice model for cleavage fracture. Failure is assumed to occur when the
fracture stress is exceeded over a characteristic distance. Taken from Ritchie, R.O., Knott, J.F., and Rice, J.R.,
‘‘On the Relationship between Critical Tensile Stress and Fracture Toughness in Mild Steel.” Journal of the
Mechanics and Physics of Solids, Vol. 21, 1973, pp. 395–410.

for the material they tested. Ritchie et al. argued that if fracture initiates in a grain boundary carbide
and propagates into a ferrite grain, the stress must be sufficient to propagate the cleavage crack across
the opposite grain boundary and into the next grain; thus σ must be exceeded over one or two grain
f
diameters. Subsequent investigations [27, 32, 33], however, revealed no consistent relationship
between the critical distance and grain size.
Curry and Knott [34] provided a statistical explanation for the RKR critical distance. A finite
volume of material must be sampled ahead of the crack tip in order to find a particle that is sufficiently
large to nucleate cleavage. Thus, a critical sample volume over which σ ≥ σ is required for failure.
f
YY
The critical volume, which can be related to a critical distance, depends on the average spacing of
cleavage nucleation sites.
The statistical argument also explains why cleavage fracture toughness data tend to be
widely scattered. Two nominally identical specimens made from the same material may display
vastly different toughness values because the location of the critical fracture-triggering particle
is random. If one specimen samples a large fracture-triggering particle near the crack tip, while
the fracture trigger in the other specimen is further from the crack tip, the latter specimen will
display a higher fracture toughness, because a higher load is required to elevate the stress at
the particle to a critical value. The statistical nature of fracture also leads to an apparent
thickness effect on toughness. A thicker specimen is more likely to sample a large fracture
trigger along the crack front, and therefore will have a lower toughness than a thin specimen,
on average [36–38].
The Curry and Knott approach was followed by more formal statistical models for cleavage
[29, 37– 40]. These models all treated cleavage as a weakest link phenomenon, where the probability
of failure is equal to the probability of sampling at least one critical fracture-triggering particle.
For a volume of material V, with ρ critical particles per unit volume, the probability of failure can
be inferred from the Poisson distribution:
F 1 −ρ V =− exp( ) (5.21)

The second term is the probability of finding zero critical particles in V, so F is the probability of
sampling one or more critical particles. The Poisson distribution can be derived from the binomial